
A ray of light is incident at an angle of incidence i, on one face of a prism of angle A (assumed to be small) and emerges normally from the opposite face. If the refractive index of the prism is \[\mu \]¸ the angle of incidence $i$ is nearly equal to
A) \[\dfrac{A}{\mu }\]
B) \[\dfrac{A}{{2\mu }}\]
C) \[\mu A\]
D) \[\dfrac{{\mu A}}{2}\]
Answer
557.7k+ views
Hint: As we know snell’s law is all about the relationship between the angle of incidence and angle refraction so Here, we will be using the formula of Snell’s law and will do some approximation wherever needed.
Formula used:
We will use Snell’s law here which is
\[\mu_1\sin i = \mu_2\sin r\]
Where $i$ is the angle of incidence and r is the angle of refraction. And \[\mu_1\& \mu_2\] are the refractive indexes of the first and second medium through which the light passes.
Complete step by step solution:
Given, the Angle of incidence of the light is $i$ on the prism. The angle of the prism is A which is to be assumed small. The ray of light emerges normally from the opposite face of the prism. And the refractive index of the prism is given which is \[\mu \].
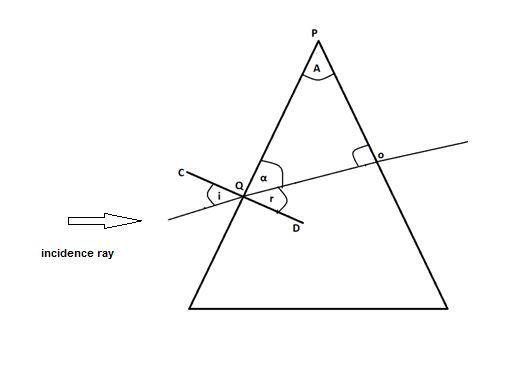
In the figure, consider triangle PQO
As we know, the sum of all angles of a triangle is equal to \[{180^ \circ }\]. So,
\[\angle {\text{PQO + }}\angle {\text{QPO + }}\angle {\text{POQ = 18}}{0^ \circ }\]
Putting \[\angle {\text{PQO = A,}}\angle {\text{QPO = }}\alpha ,\angle {\text{POQ = 9}}{{\text{0}}^ \circ }\]
So \[ \Rightarrow A + \alpha + {90^ \circ } = {180^ \circ }\]
Therefore after calculation we will get
\[ \Rightarrow \alpha = {90^ \circ } - A\]
\[ \Rightarrow A = {90^ \circ } - \alpha \] (1)
Since, CD is perpendicular on the face of the prism, So
\[\alpha + r = {90^ \circ }\]
From equation (1)
$
\Rightarrow r = {90^ \circ } - \alpha \\
\Rightarrow r = A \\
$
Therefore angle prism is equal to angle of refraction
Now, From Snell’s law,
For small angle,
i = \[\mu A\]. since sin x = x, for small angles.
Thus, we can see the angle of incidence is nearly equal to \[\mu A\].
Hence, option C is correct.
Note:
The approximation of sin function done in this solution is applicable in case of small angles only. The precisely made diagrams will give you a better understanding of the given condition.
Formula used:
We will use Snell’s law here which is
\[\mu_1\sin i = \mu_2\sin r\]
Where $i$ is the angle of incidence and r is the angle of refraction. And \[\mu_1\& \mu_2\] are the refractive indexes of the first and second medium through which the light passes.
Complete step by step solution:
Given, the Angle of incidence of the light is $i$ on the prism. The angle of the prism is A which is to be assumed small. The ray of light emerges normally from the opposite face of the prism. And the refractive index of the prism is given which is \[\mu \].

In the figure, consider triangle PQO
As we know, the sum of all angles of a triangle is equal to \[{180^ \circ }\]. So,
\[\angle {\text{PQO + }}\angle {\text{QPO + }}\angle {\text{POQ = 18}}{0^ \circ }\]
Putting \[\angle {\text{PQO = A,}}\angle {\text{QPO = }}\alpha ,\angle {\text{POQ = 9}}{{\text{0}}^ \circ }\]
So \[ \Rightarrow A + \alpha + {90^ \circ } = {180^ \circ }\]
Therefore after calculation we will get
\[ \Rightarrow \alpha = {90^ \circ } - A\]
\[ \Rightarrow A = {90^ \circ } - \alpha \] (1)
Since, CD is perpendicular on the face of the prism, So
\[\alpha + r = {90^ \circ }\]
From equation (1)
$
\Rightarrow r = {90^ \circ } - \alpha \\
\Rightarrow r = A \\
$
Therefore angle prism is equal to angle of refraction
Now, From Snell’s law,
For small angle,
i = \[\mu A\]. since sin x = x, for small angles.
Thus, we can see the angle of incidence is nearly equal to \[\mu A\].
Hence, option C is correct.
Note:
The approximation of sin function done in this solution is applicable in case of small angles only. The precisely made diagrams will give you a better understanding of the given condition.
Recently Updated Pages
The height of a solid metal cylinder is 20cm Its r-class-10-maths-ICSE

If a train crossed a pole at a speed of 60kmhr in 30 class 10 physics CBSE

Name the Writs that the High Courts are empowered to class 10 social science CBSE

A tower is 5sqrt 3 meter high Find the angle of el-class-10-maths-CBSE

Immediate cause of variations of A Mutations B Environmental class 10 biology CBSE

A rectangular container whose base is a square of side class 10 maths CBSE

Trending doubts
Why is there a time difference of about 5 hours between class 10 social science CBSE

Why is Sardar Vallabhbhai Patel called the Iron man class 10 social science CBSE

Tropical deciduous trees shed their leaves in the dry class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Write a letter to the principal requesting him to grant class 10 english CBSE

Leap year has days A 365 B 366 C 367 D 368 class 10 maths CBSE




