
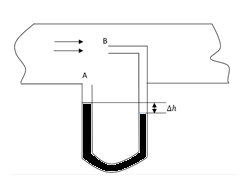
A Pitot tube (shown in the figure )is mounted along the axis of a gas pipeline whose cross-sectional area is equal to S. Assume the viscosity to be negligible, the volume of gas flowing across the section of the pipe per unit time, if the difference in the liquid columns is equal to $\Delta h$ and the densities of the liquid and gas are $\rho_o$ and $\rho$ respectively is $Q = S\sqrt {\dfrac{x\Delta g \rho_o g}{\rho}}$ find the value of x.

Answer
531.9k+ views
Hint: Apply the Bernoulli principle at the two cross-sections A and B and take the difference of the pressures at A and B equal to $\rho_o g \Delta h$ get the value of the volume of gas flowing per unit time into the section B and thus the value of the x required.
Complete step by step solution:
We have two cross-sections A and B and the gas flows through the cross-section B.
Now the Bernoulli principle can be stated as:
At any cross section the $P + \dfrac{1}{2} \rho v^2$ = constant.
Now let us consider the volume of gas flowing across section B per unit time as $V_B$
And the value of the velocity of the gas flowing through section A is zero.
Let the pressure at section A be $P_A$ and the pressure at section B is $P_B$
The density of the gas is $\rho$
Applying the Bernoulli principle in section A we get :
$P_A + \dfrac{1}{2} \rho V_A^2$ = constant
Similarly applying Bernoulli principle at section B we get:
$P_B + \dfrac{1}{2} \rho V_B^2$ = constant
Taking $V_B$ = V and $V_A$ = 0 we get from the about two equations we can get the difference in pressures as
$P_A - P_B = \dfrac{1}{2} \rho v^2$
Now we know the difference in pressure at A and B should be equal to
we get $P_A - P_B = \dfrac{1}{2} \rho v^2 = \rho _o g \Delta h$
$v = \sqrt {\dfrac{2\Delta h \rho_o g }{\rho}}$
The volume of the per unit time given area of the cross-section is: $Q = S \times v$
So we get
$Q = S \sqrt {\dfrac{2\Delta h \rho_o g }{\rho}}$
Thus we got the value of using the Bernoulli principle as 2 .
Note:Here we neglected the height difference between the section a and b. The possible mistakes that we can make in this kind of problem are that we may consider the height difference between sections A and B which will lead to mistakes and time-consuming.
Complete step by step solution:
We have two cross-sections A and B and the gas flows through the cross-section B.
Now the Bernoulli principle can be stated as:
At any cross section the $P + \dfrac{1}{2} \rho v^2$ = constant.
Now let us consider the volume of gas flowing across section B per unit time as $V_B$
And the value of the velocity of the gas flowing through section A is zero.
Let the pressure at section A be $P_A$ and the pressure at section B is $P_B$
The density of the gas is $\rho$
Applying the Bernoulli principle in section A we get :
$P_A + \dfrac{1}{2} \rho V_A^2$ = constant
Similarly applying Bernoulli principle at section B we get:
$P_B + \dfrac{1}{2} \rho V_B^2$ = constant
Taking $V_B$ = V and $V_A$ = 0 we get from the about two equations we can get the difference in pressures as
$P_A - P_B = \dfrac{1}{2} \rho v^2$
Now we know the difference in pressure at A and B should be equal to
we get $P_A - P_B = \dfrac{1}{2} \rho v^2 = \rho _o g \Delta h$
$v = \sqrt {\dfrac{2\Delta h \rho_o g }{\rho}}$
The volume of the per unit time given area of the cross-section is: $Q = S \times v$
So we get
$Q = S \sqrt {\dfrac{2\Delta h \rho_o g }{\rho}}$
Thus we got the value of using the Bernoulli principle as 2 .
Note:Here we neglected the height difference between the section a and b. The possible mistakes that we can make in this kind of problem are that we may consider the height difference between sections A and B which will lead to mistakes and time-consuming.
Recently Updated Pages
Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Why is the cell called the structural and functional class 12 biology CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Who discovered the cell and how class 12 biology CBSE

Pomato is a Somatic hybrid b Allopolyploid c Natural class 12 biology CBSE




