
A piece of paper in the shape of a sector of a circle, as shown in the figure, is rolled up to form a right circular cone.
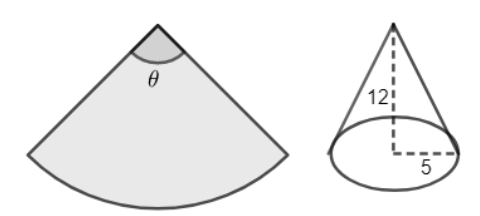
The value of the angle $\theta $ is
(a) $\dfrac{10\pi }{13}$
(b) $\dfrac{9\pi }{13}$
(c) $\dfrac{5\pi }{13}$
(d) $\dfrac{6\pi }{13}$

Answer
502.8k+ views
Hint: When a sector of circle is folded into a cone, we must remember that radius of sector of circle becomes the slant height of cone, and the length of arc of sector of circle becomes the circumference of the base of cone. We must also use the formula $\theta =\dfrac{S}{R}$, to calculate the angle where S is the length of the arc and R is the radius of the sector of the circle.
Complete step by step answer:
Let us first focus on the cone.
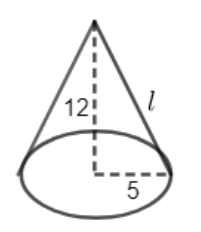
We can see that the radius of the cone is 5 units and the height of the cone is 12 units. Let the slant height of the cone be $l$ units.
So, by Pythagoras theorem, we can write
${{l}^{2}}={{5}^{2}}+{{12}^{2}}$
On taking square roots on both sides, we get
$l=\sqrt{{{5}^{2}}+{{12}^{2}}}$
Thus, we get
$l=\sqrt{25+144}$
$\Rightarrow l=\sqrt{169}$
$\Rightarrow l=13$ units.
Let us now visualize the folding of the sector of the circle to make a cone. We will notice here that the radius of the sector of the circle now becomes the slant height of the cone.
Thus, the slant height of the cone is the same as the radius of the sector of the circle.
Let the radius of the sector of the circle be R. Then we can easily write, R = 13 units.
We know that the circumference of a circle is $2\pi r$.
So, the circumference of the base of the cone is = $10\pi $.
We can see that when the sector of a circle is turned with a cone, the length of the arc of the sector of the circle becomes the circumference of the base of the cone.
Let S be the length of the arc of the sector of the circle.
So, we can say that, S = $10\pi $ units.
We know that the relation between the length of arc, radius and the angle is
$\theta =\dfrac{S}{R}$
Thus, we now have,
$\theta =\dfrac{10\pi }{13}$.
So, the correct answer is “Option a”.
Note: Here, we must remember that the angle $\theta $ is in radians and not in degrees. In this problem, we need to visualize how a sector is turned into a cone. We must understand how the radius or sector becomes the slant height and the length of the arc becomes the circumference of the base of the cone.
Complete step by step answer:
Let us first focus on the cone.

We can see that the radius of the cone is 5 units and the height of the cone is 12 units. Let the slant height of the cone be $l$ units.
So, by Pythagoras theorem, we can write
${{l}^{2}}={{5}^{2}}+{{12}^{2}}$
On taking square roots on both sides, we get
$l=\sqrt{{{5}^{2}}+{{12}^{2}}}$
Thus, we get
$l=\sqrt{25+144}$
$\Rightarrow l=\sqrt{169}$
$\Rightarrow l=13$ units.
Let us now visualize the folding of the sector of the circle to make a cone. We will notice here that the radius of the sector of the circle now becomes the slant height of the cone.
Thus, the slant height of the cone is the same as the radius of the sector of the circle.
Let the radius of the sector of the circle be R. Then we can easily write, R = 13 units.
We know that the circumference of a circle is $2\pi r$.
So, the circumference of the base of the cone is = $10\pi $.
We can see that when the sector of a circle is turned with a cone, the length of the arc of the sector of the circle becomes the circumference of the base of the cone.
Let S be the length of the arc of the sector of the circle.
So, we can say that, S = $10\pi $ units.
We know that the relation between the length of arc, radius and the angle is
$\theta =\dfrac{S}{R}$
Thus, we now have,
$\theta =\dfrac{10\pi }{13}$.
So, the correct answer is “Option a”.
Note: Here, we must remember that the angle $\theta $ is in radians and not in degrees. In this problem, we need to visualize how a sector is turned into a cone. We must understand how the radius or sector becomes the slant height and the length of the arc becomes the circumference of the base of the cone.
Recently Updated Pages
Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Trending doubts
Why is there a time difference of about 5 hours between class 10 social science CBSE

Tropical deciduous trees shed their leaves in the dry class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Write a letter to the principal requesting him to grant class 10 english CBSE

The uses of bleaching powder are A It is used bleaching class 10 chemistry CBSE

Leap year has days A 365 B 366 C 367 D 368 class 10 maths CBSE




