
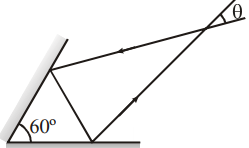
A light ray is incident on a plane mirror, which after getting reflected strikes another plane mirror, as shown in figure. The angle between the two mirrors is $60^{\circ}$. Find the angle $\theta$ is shown in figure.

Answer
452.7k+ views
Hint : In this question, we will use angle sum property. A triangle containing three angles and three sides and a pair of neighbouring sides bound each vertex. In a Euclidean period, the sum of triangle angles equals $180$ degrees. It does not matter if the triangle is obtuse, an acute, or a right triangle; the sum of all angles will be $180$ degrees. Thus, the angle sum property says that the sum of the triangle angles is equal to $180$ degrees.
Complete step-by-step solution:
The angle between the two mirrors is $60^{\circ}$.
Let $\angle A =2x$
$\angle B =2y$
This gives,
$\angle OAB =90^{\circ} - x$
$\angle OBA =90^{\circ} - y$
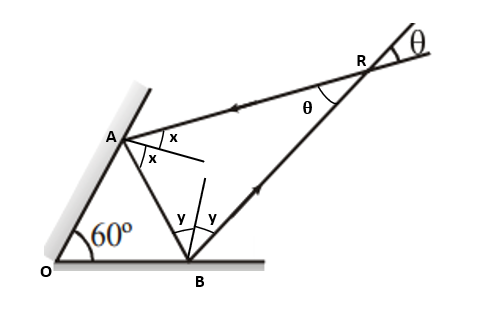
In triangle OAB,
Using sum of angle property,
$60^{\circ} + (90^{\circ} - x) +(90^{\circ} - y) = 180^{\circ} $
$\implies 60^{\circ} -x -y = 0$
$\implies x + y = 60^{\circ} $
Now, we will apply sum of angle property,
$\theta + 2x + 2y = 180^{\circ} $
Put $ x + y = 60^{\circ} $ in above formula:
$\theta + 2 (60^{\circ}) = 180^{\circ}$
$\implies \theta = 180 – 120 = 60^{\circ} $
Hence, the angle $\theta$ is $60^{\circ}$.
Note: A mirror is a reflective covering that light does not move through but bounces off, producing an image. Mirrors are formed by putting a thin coating of silver nitrate or aluminium following a smooth piece of glass. When we place an object in the face of a mirror, we see the identical object in the mirror.
Complete step-by-step solution:
The angle between the two mirrors is $60^{\circ}$.
Let $\angle A =2x$
$\angle B =2y$
This gives,
$\angle OAB =90^{\circ} - x$
$\angle OBA =90^{\circ} - y$

In triangle OAB,
Using sum of angle property,
$60^{\circ} + (90^{\circ} - x) +(90^{\circ} - y) = 180^{\circ} $
$\implies 60^{\circ} -x -y = 0$
$\implies x + y = 60^{\circ} $
Now, we will apply sum of angle property,
$\theta + 2x + 2y = 180^{\circ} $
Put $ x + y = 60^{\circ} $ in above formula:
$\theta + 2 (60^{\circ}) = 180^{\circ}$
$\implies \theta = 180 – 120 = 60^{\circ} $
Hence, the angle $\theta$ is $60^{\circ}$.
Note: A mirror is a reflective covering that light does not move through but bounces off, producing an image. Mirrors are formed by putting a thin coating of silver nitrate or aluminium following a smooth piece of glass. When we place an object in the face of a mirror, we see the identical object in the mirror.
Recently Updated Pages
Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Why is the cell called the structural and functional class 12 biology CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Who discovered the cell and how class 12 biology CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE




