
A fitness club offers weights, treadmills and aerobic classes. Fifty members were asked which services they used, and the results were as follows:
18 members use weights and do aerobics
25 members use weights and the treadmill
15 members use the treadmill and do aerobics
10 members do all the three activities
Calculate the number of members using only one of the three services.
A. 0
B. 10
C. 12
D. 18
E. 40
Answer
582.9k+ views
Hint: Assign the number of members using weight, treadmill and doing aerobics into three different sets. Generate the conditions given in the question into set operations and use the formulae of set theory using the notations for the assigned sets. Draw a Venn diagram for better visualization of mutually exclusive sets.
Complete step-by-step answer:
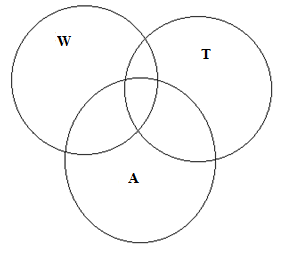
Let us assume the members using weights constitute the set W, the members using the treadmill constitute T and those doing aerobics constitute the set A.
It is given that there are all total 50 members in the fitness centre doing any of the combination of three exercises. Thus, it can be expressed in the form,
$\text{n}\left( \text{W}\bigcup{\text{T}\bigcup{\text{A}}} \right)\text{ = 50
}....\left( \text{i} \right)$
$\text{n}\left( \cdot \right)$ denotes the number of elements in a set.
Again, it is said that 18 members use weights and do aerobics. It is formulated as,
$\text{n}\left( \text{W}\bigcap{\text{A}} \right)\text{ = 18 }....\left( \text{ii} \right)$
Again, it is said that 25 members use weights and treadmill. It is formulated as,
$\text{n}\left( \text{W}\bigcap{\text{T}} \right)\text{ = 25 }....\text{(iii)}$
Again, it is said that 15 members use the treadmill and do aerobics. It is formulated as,
$\text{n}\left( \text{T}\bigcap{\text{A}} \right)\text{ = 15 }....\left( \text{iv} \right)$
Finally, it is said that 10 members take part in all three exercises. Thus,
$\text{n}\left( \text{W}\bigcap{\text{T}\bigcap{\text{A}}} \right)\text{ = 10
}....\left( \text{v} \right)$
We know, from a Venn diagram that, for any two sets A and B, in the presence of a
third set C , $\text{A}\bigcap{\text{B = }\left(
\text{A}\bigcap{\text{B}}\bigcap{\text{C}} \right)\bigcup{\left(
\text{A}\bigcap{\text{B}\bigcap{{{\text{C}}^{^{c}}}}} \right)}}$,
where,${{\text{C}}^{c}}$is the complement of any set C.
Therefore, we can say,
$\text{n}\left( \text{A}\bigcap{\text{B}} \right)\text{ = n}\left(
\text{A}\bigcap{\text{B}}\bigcap{\text{C}} \right)\text{ + n}\left(
\text{A}\bigcap{\text{B}\bigcap{{{\text{C}}^{^{c}}}}} \right)$ (since, the two sets
are mutually exclusive)
Thus, adding (ii), (iii) and (iv), we get,
$\begin{align}
& \text{n}\left( \text{W}\bigcap{\text{A}} \right)\text{ + n}\left(
\text{W}\bigcap{\text{T}} \right)\text{ + n}\left( \text{T}\bigcap{\text{A}}
\right)\text{ = 58} \\
& \Rightarrow \text{ n}\left( \text{W}\bigcap{\text{T}}\bigcap{\text{A}}
\right)\text{ + n}\left( \text{W}\bigcap{{{\text{T}}^{c}}\bigcap{\text{A}}}
\right)\text{ + n}\left( \text{W}\bigcap{\text{T}}\bigcap{\text{A}} \right)\text{ +
n}\left( \text{W}\bigcap{\text{T}\bigcap{{{\text{A}}^{c}}}} \right)\text{ + n}\left(
\text{W}\bigcap{\text{T}}\bigcap{\text{A}} \right)\text{ } \\
& \text{ + n}\left( {{\text{W}}^{c}}\bigcap{\text{T}\bigcap{\text{A}}}
\right)\text{ = 58} \\
& \Rightarrow \text{ n}\left( \text{W}\bigcap{{{\text{T}}^{c}}\bigcap{\text{A}}}
\right)\text{ }+\text{ n}\left( \text{W}\bigcap{\text{T}\bigcap{{{\text{A}}^{c}}}}
\right)\text{ + n}\left( {{\text{W}}^{c}}\bigcap{\text{T}\bigcap{\text{A}}}
\right)\text{ = 58 }-\text{ 3*10 }\left( \because \text{ n}\left(
\text{W}\bigcap{\text{T}}\bigcap{\text{A}} \right)=10 \right) \\
& \therefore \text{ n}\left( \text{W}\bigcap{{{\text{T}}^{c}}\bigcap{\text{A}}}
\right)\text{ }+\text{ n}\left( \text{W}\bigcap{\text{T}\bigcap{{{\text{A}}^{c}}}}
\right)\text{ + n}\left( {{\text{W}}^{c}}\bigcap{\text{T}\bigcap{\text{A}}}
\right)=\text{ }28 \\
\end{align}$Thus, there are 28 members participating in exactly two of the three
exercises.
Thus, it is evident from the Venn diagram, to calculate the number of members
participating in exactly one of the three exercises, we need to subtract the members
who participate exactly in two exercises and all the three exercises from the total
number of members.
$\therefore $Number of members participating in exactly one of the three exercises
$\begin{align}
& =\text{ 58 }-\text{ 28 }-\text{ }10 \\
& =\text{ 12} \\
\end{align}$
Thus, 12 members participate in exactly one of the three exercises.
Note: It is always advisable to draw a Venn diagram to visualize the mutually
exclusive sections of the sets.
Complete step-by-step answer:

Let us assume the members using weights constitute the set W, the members using the treadmill constitute T and those doing aerobics constitute the set A.
It is given that there are all total 50 members in the fitness centre doing any of the combination of three exercises. Thus, it can be expressed in the form,
$\text{n}\left( \text{W}\bigcup{\text{T}\bigcup{\text{A}}} \right)\text{ = 50
}....\left( \text{i} \right)$
$\text{n}\left( \cdot \right)$ denotes the number of elements in a set.
Again, it is said that 18 members use weights and do aerobics. It is formulated as,
$\text{n}\left( \text{W}\bigcap{\text{A}} \right)\text{ = 18 }....\left( \text{ii} \right)$
Again, it is said that 25 members use weights and treadmill. It is formulated as,
$\text{n}\left( \text{W}\bigcap{\text{T}} \right)\text{ = 25 }....\text{(iii)}$
Again, it is said that 15 members use the treadmill and do aerobics. It is formulated as,
$\text{n}\left( \text{T}\bigcap{\text{A}} \right)\text{ = 15 }....\left( \text{iv} \right)$
Finally, it is said that 10 members take part in all three exercises. Thus,
$\text{n}\left( \text{W}\bigcap{\text{T}\bigcap{\text{A}}} \right)\text{ = 10
}....\left( \text{v} \right)$
We know, from a Venn diagram that, for any two sets A and B, in the presence of a
third set C , $\text{A}\bigcap{\text{B = }\left(
\text{A}\bigcap{\text{B}}\bigcap{\text{C}} \right)\bigcup{\left(
\text{A}\bigcap{\text{B}\bigcap{{{\text{C}}^{^{c}}}}} \right)}}$,
where,${{\text{C}}^{c}}$is the complement of any set C.
Therefore, we can say,
$\text{n}\left( \text{A}\bigcap{\text{B}} \right)\text{ = n}\left(
\text{A}\bigcap{\text{B}}\bigcap{\text{C}} \right)\text{ + n}\left(
\text{A}\bigcap{\text{B}\bigcap{{{\text{C}}^{^{c}}}}} \right)$ (since, the two sets
are mutually exclusive)
Thus, adding (ii), (iii) and (iv), we get,
$\begin{align}
& \text{n}\left( \text{W}\bigcap{\text{A}} \right)\text{ + n}\left(
\text{W}\bigcap{\text{T}} \right)\text{ + n}\left( \text{T}\bigcap{\text{A}}
\right)\text{ = 58} \\
& \Rightarrow \text{ n}\left( \text{W}\bigcap{\text{T}}\bigcap{\text{A}}
\right)\text{ + n}\left( \text{W}\bigcap{{{\text{T}}^{c}}\bigcap{\text{A}}}
\right)\text{ + n}\left( \text{W}\bigcap{\text{T}}\bigcap{\text{A}} \right)\text{ +
n}\left( \text{W}\bigcap{\text{T}\bigcap{{{\text{A}}^{c}}}} \right)\text{ + n}\left(
\text{W}\bigcap{\text{T}}\bigcap{\text{A}} \right)\text{ } \\
& \text{ + n}\left( {{\text{W}}^{c}}\bigcap{\text{T}\bigcap{\text{A}}}
\right)\text{ = 58} \\
& \Rightarrow \text{ n}\left( \text{W}\bigcap{{{\text{T}}^{c}}\bigcap{\text{A}}}
\right)\text{ }+\text{ n}\left( \text{W}\bigcap{\text{T}\bigcap{{{\text{A}}^{c}}}}
\right)\text{ + n}\left( {{\text{W}}^{c}}\bigcap{\text{T}\bigcap{\text{A}}}
\right)\text{ = 58 }-\text{ 3*10 }\left( \because \text{ n}\left(
\text{W}\bigcap{\text{T}}\bigcap{\text{A}} \right)=10 \right) \\
& \therefore \text{ n}\left( \text{W}\bigcap{{{\text{T}}^{c}}\bigcap{\text{A}}}
\right)\text{ }+\text{ n}\left( \text{W}\bigcap{\text{T}\bigcap{{{\text{A}}^{c}}}}
\right)\text{ + n}\left( {{\text{W}}^{c}}\bigcap{\text{T}\bigcap{\text{A}}}
\right)=\text{ }28 \\
\end{align}$Thus, there are 28 members participating in exactly two of the three
exercises.
Thus, it is evident from the Venn diagram, to calculate the number of members
participating in exactly one of the three exercises, we need to subtract the members
who participate exactly in two exercises and all the three exercises from the total
number of members.
$\therefore $Number of members participating in exactly one of the three exercises
$\begin{align}
& =\text{ 58 }-\text{ 28 }-\text{ }10 \\
& =\text{ 12} \\
\end{align}$
Thus, 12 members participate in exactly one of the three exercises.
Note: It is always advisable to draw a Venn diagram to visualize the mutually
exclusive sections of the sets.
Recently Updated Pages
How do you convert r6sec theta into Cartesian form class 10 maths CBSE

How do you solve dfrac5y3dfracy+72y6+1 and find any class 10 maths CBSE

If sin A+B1 and cos AB1 0circ le left A+B rightle 90circ class 10 maths CBSE

On the number line 10 is to the of zero class 10 maths CBSE

How do you solve 5xge 30 class 10 maths CBSE

In the following sentence supply a verb in agreement class 10 english CBSE

Trending doubts
Write an application to the principal requesting five class 10 english CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What is the median of the first 10 natural numbers class 10 maths CBSE

Write examples of herbivores carnivores and omnivo class 10 biology CBSE




