
A farmer moves along the boundary of a square field of side 10m in 40s. What will be the magnitude of displacement of the farmer at the end of 2 minutes 20 seconds from his initial position?
Answer
455.7k+ views
Hint: Calculate the net distance travelled by the farmer using the given values and then use it to find the point on the square which is the final position of the farmer. The length of the line joining directly the initial and final position of the farmer is the net displacement.
Complete step-by-step answer:
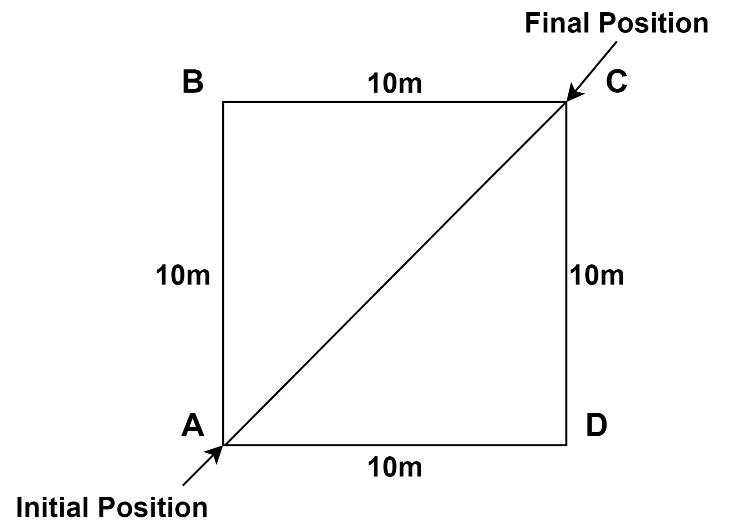
Given the problem, a farmer moves along the boundary of a square field of side 10m in 40 seconds.
We need to find the magnitude of displacement of the farmer at the end of 2 minutes 20 seconds from his initial position.
First, we calculate the perimeter of the square.
The side of square $ABCD$ is $x = 10m$.
Perimeter of the square $ = 4 \times side = 4x = 4 \times 10 = 40m$.
It is given that the farmer takes 40 seconds to complete one round of this square field.
Hence the distance travelled by the farmer in 40 seconds is $40m$.
We know that ${\text{speed}} = \dfrac{{{\text{distance}}}}{{{\text{time}}}}$.
Using the above values in this formula we get,
Speed of farmer$ = \dfrac{{40m}}{{40s}} = 1{\text{ }}m/s$.
Now we need to calculate the distance travelled by the farmer in 2 minutes 20 seconds or 140 seconds.
Using the same speed formula, we get
$
{\text{speed}} = \dfrac{{{\text{distance}}}}{{{\text{time}}}} \\
\Rightarrow 1 = \dfrac{{{\text{distance}}}}{{140}} \\
\Rightarrow {\text{distance = }}140m \\
$
Hence the distance travelled by the farmer in 2 minutes 20 seconds is 140m.
Now we need to calculate the position of the farmer on the boundary of square $ABCD$ after 2 minutes 20 seconds.
We know that,
Perimeter of the square = One round of the square
$ \Rightarrow 40m = 1{\text{ round}}$
$
\Rightarrow 1m = \dfrac{1}{{40}}{\text{ round}} \\
\Rightarrow 140m = \dfrac{1}{{40}} \times 140 = 3.5{\text{ rounds}} \\
$
Hence the farmer completes 3.5 rounds of the square field $ABCD$ in 2 minutes 20 seconds.
When the farmer completes one round of square field $ABCD$ starting from vertex $A$
clockwise, after completion the net displacement from the starting position is zero.
Hence the net displacement after the completion of 3 rounds is also zero.
After 0.5 rounds, the farmer reaches the diagonally opposite point of the starting position,
that is if the farmer starts from vertex $A$ of square field $ABCD$, it reaches to point $C$.
The net displacement from the starting point is equal to the diagonal $AC$ of the square
field.
Hence the net displacement if the farmer after 3.5 rounds is equal to the diagonal $AC$ of the square field.
Applying Pythagoras theorem in right angle triangle $ADC$, we get
$
{\text{Hypotenus}}{{\text{e}}^2} = {\text{Bas}}{{\text{e}}^2} + {\text{Heigh}}{{\text{t}}^2} \\
\Rightarrow A{C^2} = A{D^2} + D{C^2} \\
\Rightarrow A{C^2} = {10^2} + {10^2} = 200 \\
\Rightarrow AC = \sqrt {200} = 10\sqrt 2 m \\
$
Hence the net displacement if the farmer after 3.5 rounds is equal to $10\sqrt 2 m$.
Therefore, the magnitude of displacement of the farmer at the end of 2 minutes 20 seconds from his initial position is $10\sqrt 2 m$.
Note: The length of the actual path covered by a body is called the distance covered. The length of the shortest path possible between the initial and final position of the body is called its displacement. Displacement is always less than equal to the distance covered by the body. Visual description in problems like above helps in solving the problem easily.
Complete step-by-step answer:

Given the problem, a farmer moves along the boundary of a square field of side 10m in 40 seconds.
We need to find the magnitude of displacement of the farmer at the end of 2 minutes 20 seconds from his initial position.
First, we calculate the perimeter of the square.
The side of square $ABCD$ is $x = 10m$.
Perimeter of the square $ = 4 \times side = 4x = 4 \times 10 = 40m$.
It is given that the farmer takes 40 seconds to complete one round of this square field.
Hence the distance travelled by the farmer in 40 seconds is $40m$.
We know that ${\text{speed}} = \dfrac{{{\text{distance}}}}{{{\text{time}}}}$.
Using the above values in this formula we get,
Speed of farmer$ = \dfrac{{40m}}{{40s}} = 1{\text{ }}m/s$.
Now we need to calculate the distance travelled by the farmer in 2 minutes 20 seconds or 140 seconds.
Using the same speed formula, we get
$
{\text{speed}} = \dfrac{{{\text{distance}}}}{{{\text{time}}}} \\
\Rightarrow 1 = \dfrac{{{\text{distance}}}}{{140}} \\
\Rightarrow {\text{distance = }}140m \\
$
Hence the distance travelled by the farmer in 2 minutes 20 seconds is 140m.
Now we need to calculate the position of the farmer on the boundary of square $ABCD$ after 2 minutes 20 seconds.
We know that,
Perimeter of the square = One round of the square
$ \Rightarrow 40m = 1{\text{ round}}$
$
\Rightarrow 1m = \dfrac{1}{{40}}{\text{ round}} \\
\Rightarrow 140m = \dfrac{1}{{40}} \times 140 = 3.5{\text{ rounds}} \\
$
Hence the farmer completes 3.5 rounds of the square field $ABCD$ in 2 minutes 20 seconds.
When the farmer completes one round of square field $ABCD$ starting from vertex $A$
clockwise, after completion the net displacement from the starting position is zero.
Hence the net displacement after the completion of 3 rounds is also zero.
After 0.5 rounds, the farmer reaches the diagonally opposite point of the starting position,
that is if the farmer starts from vertex $A$ of square field $ABCD$, it reaches to point $C$.
The net displacement from the starting point is equal to the diagonal $AC$ of the square
field.
Hence the net displacement if the farmer after 3.5 rounds is equal to the diagonal $AC$ of the square field.
Applying Pythagoras theorem in right angle triangle $ADC$, we get
$
{\text{Hypotenus}}{{\text{e}}^2} = {\text{Bas}}{{\text{e}}^2} + {\text{Heigh}}{{\text{t}}^2} \\
\Rightarrow A{C^2} = A{D^2} + D{C^2} \\
\Rightarrow A{C^2} = {10^2} + {10^2} = 200 \\
\Rightarrow AC = \sqrt {200} = 10\sqrt 2 m \\
$
Hence the net displacement if the farmer after 3.5 rounds is equal to $10\sqrt 2 m$.
Therefore, the magnitude of displacement of the farmer at the end of 2 minutes 20 seconds from his initial position is $10\sqrt 2 m$.
Note: The length of the actual path covered by a body is called the distance covered. The length of the shortest path possible between the initial and final position of the body is called its displacement. Displacement is always less than equal to the distance covered by the body. Visual description in problems like above helps in solving the problem easily.
Recently Updated Pages
Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Class 10 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Economics: Engaging Questions & Answers for Success

Trending doubts
Why is there a time difference of about 5 hours between class 10 social science CBSE

What is the scientific name of apple class 10 biology CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Fill the blanks with proper collective nouns 1 A of class 10 english CBSE

Write examples of herbivores carnivores and omnivo class 10 biology CBSE

Give 10 examples of Material nouns Abstract nouns Common class 10 english CBSE




