
A charged particle of specific charge $\alpha $ is released from origin at time t=0 with velocity $\overrightarrow V = {V_0}\widehat i$ in a uniform magnetic field $\overrightarrow B = {B_0}\widehat k$. If the particle passes through $\left( {0,y,0} \right)$, then y is equal to (specific charge $\alpha = q/m$)
A. $\dfrac{{2{V_0}}}{{\alpha {B_0}}}$
B. $ - \dfrac{{3{V_0}}}{{\alpha {B_0}}}$
C. $ - \dfrac{{2{V_0}}}{{\alpha {B_0}}}$
D. $ - \dfrac{{6{V_0}}}{{\alpha {B_0}}}$
Answer
525.3k+ views
Hint: Any charged particle, in presence of a magnetic field, experiences a force in the direction perpendicular to both the velocity and the magnetic field. This leads to a charged particle moving a circular motion. To find the y-coordinate we need to find the radius of this circle.
Formula used:
$R = \dfrac{{m{V_0}}}{{q{B_0}}}$
Complete answer:
In the question, they’ve given a specific charge of $\alpha $ which is released at the origin. At time t=0, the particle is moving in the direction of the positive x-axis. But the magnetic field intensity is acting in the direction of the positive z-axis, which is into the plane of the paper. So, from the right-hand rule, the magnetic force will keep moving in a circular motion, with some radius.
The charged particle’s motion would look something like this.
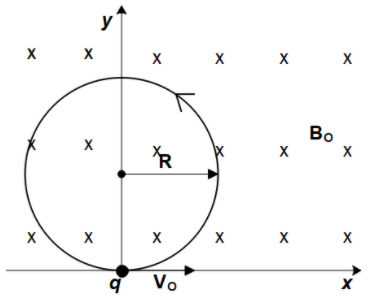
Now, we can clearly see that the magnetic force ${F_B}$, is supplying the necessary centripetal force ${F_C}$. This can be written as
$\eqalign{
& {F_B} = {F_C} \cr
& \Rightarrow q{V_0}{B_0} = \dfrac{{m{V_0}^2}}{R} \cr
& \Rightarrow R = \dfrac{{m{V_0}}}{{q{B_0}}} \cr} $
They’ve already mentioned in the problem, that the specific charge of the particle is $\alpha = q/m$. So,
$\eqalign{
& R = \dfrac{{m{V_0}}}{{q{B_0}}} \cr
& \Rightarrow R = \dfrac{{{V_0}}}{{\alpha {B_0}}} \cr} $
Thus, the particle will be moving in a circular motion of radius R, in the XY plane with the center on the y-axis. The particle will thus pass through a point on the y-axis which will be the diameter of the circle. So the coordinates of the point will be $(0,2R,0)$ which is nothing but $\left( {0,\dfrac{{2{V_0}}}{{\alpha {B_0}}},0} \right)$.
Therefore, the y coordinates of the particle will be $\dfrac{{2{V_0}}}{{\alpha {B_0}}}$.
Thus, the correct option is A.
Note:
The circular path of the charged particle can be traced from Fleming’s right-hand rule by applying it at either end of the diameter of the circle. Here, you must observe that the velocity of the charged particle is not subject to change. The magnetic field will only vary the direction. No work is done by the magnetic field.
Formula used:
$R = \dfrac{{m{V_0}}}{{q{B_0}}}$
Complete answer:
In the question, they’ve given a specific charge of $\alpha $ which is released at the origin. At time t=0, the particle is moving in the direction of the positive x-axis. But the magnetic field intensity is acting in the direction of the positive z-axis, which is into the plane of the paper. So, from the right-hand rule, the magnetic force will keep moving in a circular motion, with some radius.
The charged particle’s motion would look something like this.

Now, we can clearly see that the magnetic force ${F_B}$, is supplying the necessary centripetal force ${F_C}$. This can be written as
$\eqalign{
& {F_B} = {F_C} \cr
& \Rightarrow q{V_0}{B_0} = \dfrac{{m{V_0}^2}}{R} \cr
& \Rightarrow R = \dfrac{{m{V_0}}}{{q{B_0}}} \cr} $
They’ve already mentioned in the problem, that the specific charge of the particle is $\alpha = q/m$. So,
$\eqalign{
& R = \dfrac{{m{V_0}}}{{q{B_0}}} \cr
& \Rightarrow R = \dfrac{{{V_0}}}{{\alpha {B_0}}} \cr} $
Thus, the particle will be moving in a circular motion of radius R, in the XY plane with the center on the y-axis. The particle will thus pass through a point on the y-axis which will be the diameter of the circle. So the coordinates of the point will be $(0,2R,0)$ which is nothing but $\left( {0,\dfrac{{2{V_0}}}{{\alpha {B_0}}},0} \right)$.
Therefore, the y coordinates of the particle will be $\dfrac{{2{V_0}}}{{\alpha {B_0}}}$.
Thus, the correct option is A.
Note:
The circular path of the charged particle can be traced from Fleming’s right-hand rule by applying it at either end of the diameter of the circle. Here, you must observe that the velocity of the charged particle is not subject to change. The magnetic field will only vary the direction. No work is done by the magnetic field.
Recently Updated Pages
Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Why is the cell called the structural and functional class 12 biology CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Who discovered the cell and how class 12 biology CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE




