
A boiler is in the form of a cylinder 2m long with hemispherical ends each of 2 metre diameter. Find the volume of the boiler.
Answer
553.2k+ views
Hint: In this question we have to find Volume of the boiler. First step is to draw a diagram. It will give us a clear picture of what to find out, considering the given quantity, break the diagram into 3 parts, two hemispheres and one cylinder. Now using the formula of volume of a cylinder and hemisphere you will get the final answer.
Complete step-by-step answer:
According to the question, a boiler is in the form of a cylinder 2 m long with hemispherical ends each of 2 metre diameter.
The height of the cylinder is h and the radius of the cylinder is r.
Height of the cylinder = h = 2 m
Diameter of the hemisphere = 2 m
As we know that Radius = $\dfrac{{{\rm{Diameter}}}}{2}$
∴ Radius of the hemisphere = ${\rm{r}} = \dfrac{{{\rm{Diameter}}}}{2} = \dfrac{2}{2} = 1{\rm{m}}$
Since at ends of cylinder hemisphere are attached,
So, Radius of the Cylinder = Radius of the hemisphere = r = 1m
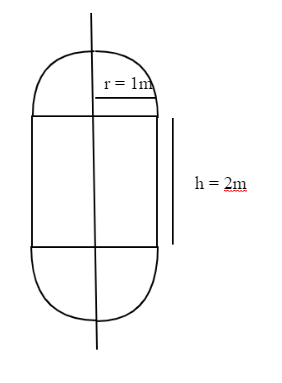
From above diagram,
Total volume of the boiler = Volume of the cylindrical portion + Volume of the two hemispheres
We know that,
Volume of the cylinder = ${\rm{\pi }}{{\rm{r}}^2}{\rm{h}}$
Volume of the hemisphere = $\dfrac{{2{\rm{\;\pi }}{{\rm{r}}^3}}}{3}$
Now,
Total volume of the boiler = ${\rm{V\;}} = {\rm{\;\pi }}{{\rm{r}}^2}{\rm{h\;}} + {\rm{\;}}2 \times \left( {\dfrac{{2{\rm{\;\pi }}{{\rm{r}}^3}}}{3}} \right)$
$ \Rightarrow {\rm{V\;}} = {\rm{\;\pi }}{{\rm{r}}^2}{\rm{h\;}} + \dfrac{4}{3}{\rm{\pi }}{{\rm{r}}^3}$
$ \Rightarrow {\rm{V\;}} = {\rm{\;\pi }}{{\rm{r}}^2}\left( {{\rm{h\;}} + \dfrac{{4{\rm{r}}}}{3}} \right)$
$ \Rightarrow {\rm{V\;}} = \dfrac{{22}}{7} \times {\rm{\;}}{1^2} \times \left( {{\rm{\;}}2{\rm{\;}} + \dfrac{4}{3} \times 1} \right)$
$ \Rightarrow {\rm{V\;}} = \dfrac{{22}}{7} \times \left( {\dfrac{{6 + 4}}{3}} \right)$
$ \Rightarrow {\rm{V\;}} = \dfrac{{22}}{7} \times \dfrac{{10}}{3}{\rm{\;}} = \dfrac{{220}}{{21}}$
Therefore, Volume of the boiler is $\dfrac{{220}}{{21}}$ m³
Note: Whenever we face such types of problems the key concept is to draw the pictorial representation of the given problem and then split into parts such that we can use the formula of standard quantities in order to get the volume of the boiler.
Complete step-by-step answer:
According to the question, a boiler is in the form of a cylinder 2 m long with hemispherical ends each of 2 metre diameter.
The height of the cylinder is h and the radius of the cylinder is r.
Height of the cylinder = h = 2 m
Diameter of the hemisphere = 2 m
As we know that Radius = $\dfrac{{{\rm{Diameter}}}}{2}$
∴ Radius of the hemisphere = ${\rm{r}} = \dfrac{{{\rm{Diameter}}}}{2} = \dfrac{2}{2} = 1{\rm{m}}$
Since at ends of cylinder hemisphere are attached,
So, Radius of the Cylinder = Radius of the hemisphere = r = 1m

From above diagram,
Total volume of the boiler = Volume of the cylindrical portion + Volume of the two hemispheres
We know that,
Volume of the cylinder = ${\rm{\pi }}{{\rm{r}}^2}{\rm{h}}$
Volume of the hemisphere = $\dfrac{{2{\rm{\;\pi }}{{\rm{r}}^3}}}{3}$
Now,
Total volume of the boiler = ${\rm{V\;}} = {\rm{\;\pi }}{{\rm{r}}^2}{\rm{h\;}} + {\rm{\;}}2 \times \left( {\dfrac{{2{\rm{\;\pi }}{{\rm{r}}^3}}}{3}} \right)$
$ \Rightarrow {\rm{V\;}} = {\rm{\;\pi }}{{\rm{r}}^2}{\rm{h\;}} + \dfrac{4}{3}{\rm{\pi }}{{\rm{r}}^3}$
$ \Rightarrow {\rm{V\;}} = {\rm{\;\pi }}{{\rm{r}}^2}\left( {{\rm{h\;}} + \dfrac{{4{\rm{r}}}}{3}} \right)$
$ \Rightarrow {\rm{V\;}} = \dfrac{{22}}{7} \times {\rm{\;}}{1^2} \times \left( {{\rm{\;}}2{\rm{\;}} + \dfrac{4}{3} \times 1} \right)$
$ \Rightarrow {\rm{V\;}} = \dfrac{{22}}{7} \times \left( {\dfrac{{6 + 4}}{3}} \right)$
$ \Rightarrow {\rm{V\;}} = \dfrac{{22}}{7} \times \dfrac{{10}}{3}{\rm{\;}} = \dfrac{{220}}{{21}}$
Therefore, Volume of the boiler is $\dfrac{{220}}{{21}}$ m³
Note: Whenever we face such types of problems the key concept is to draw the pictorial representation of the given problem and then split into parts such that we can use the formula of standard quantities in order to get the volume of the boiler.
Recently Updated Pages
Physics and Measurement Mock Test 2025 – Practice Questions & Answers

NCERT Solutions For Class 5 English Marigold - The Little Bully

NCERT Solutions For Class 12 Maths Three Dimensional Geometry Exercise 11.1

NCERT Solutions For Class 11 English Woven Words (Poem) - Ajamil And The Tigers

NCERT Solutions For Class 6 Hindi Durva - Bhaaloo

NCERT Solutions For Class 12 Physics In Hindi - Wave Optics

Trending doubts
Why is there a time difference of about 5 hours between class 10 social science CBSE

Fill the blanks with proper collective nouns 1 A of class 10 english CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

When the President submits his resignation to the VicePresident class 10 social science CBSE

Five things I will do to build a great India class 10 english CBSE

Write examples of herbivores carnivores and omnivo class 10 biology CBSE




