
A 25watt, 220 volt bulb and 100 watt, 220 volt bulbs are connected in series across 440 volt lines.
A) Only 100 watt bulb will fuse
B) Only 25 watt bulb will fuse
C) None of these bulbs will fuse
D) Both bulbs will fuse
Answer
523.5k+ views
Hint:In such types of questions first we calculate the resistance of the bulb and the maximum current which can flow from the bulb. If the current flown in the whole circuit is greater than the maximum current of the bulb in that condition the bulb will fuse.
Complete step-by-step answer:
We have two bulb marked as ${P_1} = 25w$ $220V$ and ${P_2} = 100w$ $220V$ are connected in series with $440V$ source as given below
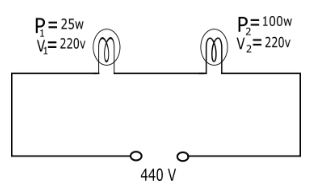
Step 1
First we calculate the resistance of both bulbs.
We know $P = \dfrac{{{V^2}}}{R}$ where $P \Rightarrow $ power of bulb which marked on bulb
$V \Rightarrow $ Voltage marked on bulb
$R \Rightarrow $ Resistance of bulb which always remain same
For bulb $B_1$
$
{P_1} = 25w \\
{V_1} = 220V \\
$
So ${P_1} = \dfrac{{{V_1}^2}}{{{R_1}}}$
Put value in this formula
$ \Rightarrow 25 = \dfrac{{{{220}^2}}}{{{R_1}}}$
$ \Rightarrow 25 = \dfrac{{48400}}{{{R_1}}}$
$ \Rightarrow {R_1} = \dfrac{{48400}}{{25}}$
By solving this
$ \Rightarrow {R_1} = 1936\Omega $
This is the resistance of Bulb 1
Now for second bulb
$
{P_2} = 100w \\
{V_2} = 220V \\
$
Apply same method
${P_2} = \dfrac{{{V_2}^2}}{{{R_2}}}$
$ \Rightarrow 100 = \dfrac{{{{220}^2}}}{{{R_1}}}$
By solving this
$ \Rightarrow {R_2} = \dfrac{{48400}}{{100}}$
$ \Rightarrow {R_2} = 484\Omega $
We get the resistance of both bulb is ${R_1} = 1936\Omega $ ${R_2} = 484\Omega $
Step 2
In this step we calculate the maximum current which can flow from bulb 1 and bulb 2 without damaging them
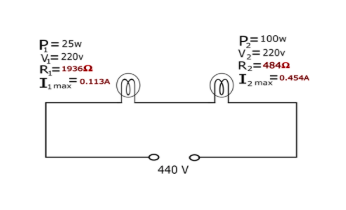
Maximum current can flow from bulb can find with the help of formula $P = V \times I$
Where $P \Rightarrow $ power of bulb
$V \Rightarrow $ Voltage of bulb which given on bulb
Apply this formula for both bulbs
For bulb $B_1$
${P_1} = {V_1} \times {I_{1\max }}$
$ \Rightarrow 25 = 220 \times {I_{1\max }}$
$ \Rightarrow {I_{1\max }} = \dfrac{{25}}{{220}}$
By solving this
$ \Rightarrow {I_{1\max }} = 0.113A$
Now for $B_2$
${P_2} = {V_2} \times {I_{2\max }}$
$ \Rightarrow 100 = 220 \times {I_{2\max }}$
$ \Rightarrow {I_{1\max }} = \dfrac{{100}}{{220}}$
By solving this
$ \Rightarrow {I_{1\max }} = 0.454A$
In this step we get the maximum current for both bulbs which can flow through bulb easily without damaging them
Step 3
In this step we will calculate the current flow from the whole circuit when bulbs connected in series with 440V supply
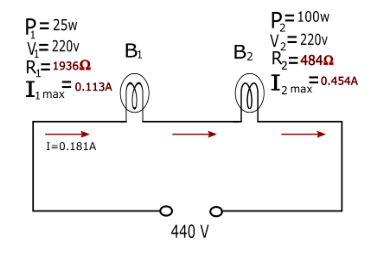
Resultant resistance of this circuit is $R = {R_1} + {R_2}$
$ \Rightarrow R = 1936\Omega + 484\Omega $
$ \Rightarrow R = 2420\Omega $
We know $V = I \times R$
Where $V \Rightarrow $ voltage given in supply
Put the value and solving
$ \Rightarrow 440 = I \times 2420$
$ \Rightarrow I = \dfrac{{440}}{{2420}}$
Further solving
$ \Rightarrow I = 0.181A$
Step 4
Now we clearly see that the current flow by 440 V source is $0.181A$
Which is exceeds the ${I_{1\max }} = 0.113A$ so the bulb 1 can not bear this much current so it will fuse but the ${I_{2\max }} = 0.454A$ is greater than current flow by supply so bulb 2 will not fuse.
Bulb 1 ${I_{1\max }} < I \Rightarrow $ fuse
Bulb 2 ${I_{2\max }} > I \Rightarrow $ not fuse
Hence in this question option B is correct.
Note:As we see if we want to solve such type of question then we have to find the current which a bulb can bear if the battery gives more current in the circuit if bulb connected in series the current in both bulb is same as current flowing in circuit than in that condition filament of bulb get heat and melt and finally that bulb will be fuse.
Complete step-by-step answer:
We have two bulb marked as ${P_1} = 25w$ $220V$ and ${P_2} = 100w$ $220V$ are connected in series with $440V$ source as given below

Step 1
First we calculate the resistance of both bulbs.
We know $P = \dfrac{{{V^2}}}{R}$ where $P \Rightarrow $ power of bulb which marked on bulb
$V \Rightarrow $ Voltage marked on bulb
$R \Rightarrow $ Resistance of bulb which always remain same
For bulb $B_1$
$
{P_1} = 25w \\
{V_1} = 220V \\
$
So ${P_1} = \dfrac{{{V_1}^2}}{{{R_1}}}$
Put value in this formula
$ \Rightarrow 25 = \dfrac{{{{220}^2}}}{{{R_1}}}$
$ \Rightarrow 25 = \dfrac{{48400}}{{{R_1}}}$
$ \Rightarrow {R_1} = \dfrac{{48400}}{{25}}$
By solving this
$ \Rightarrow {R_1} = 1936\Omega $
This is the resistance of Bulb 1
Now for second bulb
$
{P_2} = 100w \\
{V_2} = 220V \\
$
Apply same method
${P_2} = \dfrac{{{V_2}^2}}{{{R_2}}}$
$ \Rightarrow 100 = \dfrac{{{{220}^2}}}{{{R_1}}}$
By solving this
$ \Rightarrow {R_2} = \dfrac{{48400}}{{100}}$
$ \Rightarrow {R_2} = 484\Omega $
We get the resistance of both bulb is ${R_1} = 1936\Omega $ ${R_2} = 484\Omega $
Step 2
In this step we calculate the maximum current which can flow from bulb 1 and bulb 2 without damaging them

Maximum current can flow from bulb can find with the help of formula $P = V \times I$
Where $P \Rightarrow $ power of bulb
$V \Rightarrow $ Voltage of bulb which given on bulb
Apply this formula for both bulbs
For bulb $B_1$
${P_1} = {V_1} \times {I_{1\max }}$
$ \Rightarrow 25 = 220 \times {I_{1\max }}$
$ \Rightarrow {I_{1\max }} = \dfrac{{25}}{{220}}$
By solving this
$ \Rightarrow {I_{1\max }} = 0.113A$
Now for $B_2$
${P_2} = {V_2} \times {I_{2\max }}$
$ \Rightarrow 100 = 220 \times {I_{2\max }}$
$ \Rightarrow {I_{1\max }} = \dfrac{{100}}{{220}}$
By solving this
$ \Rightarrow {I_{1\max }} = 0.454A$
In this step we get the maximum current for both bulbs which can flow through bulb easily without damaging them
Step 3
In this step we will calculate the current flow from the whole circuit when bulbs connected in series with 440V supply

Resultant resistance of this circuit is $R = {R_1} + {R_2}$
$ \Rightarrow R = 1936\Omega + 484\Omega $
$ \Rightarrow R = 2420\Omega $
We know $V = I \times R$
Where $V \Rightarrow $ voltage given in supply
Put the value and solving
$ \Rightarrow 440 = I \times 2420$
$ \Rightarrow I = \dfrac{{440}}{{2420}}$
Further solving
$ \Rightarrow I = 0.181A$
Step 4
Now we clearly see that the current flow by 440 V source is $0.181A$
Which is exceeds the ${I_{1\max }} = 0.113A$ so the bulb 1 can not bear this much current so it will fuse but the ${I_{2\max }} = 0.454A$ is greater than current flow by supply so bulb 2 will not fuse.
Bulb 1 ${I_{1\max }} < I \Rightarrow $ fuse
Bulb 2 ${I_{2\max }} > I \Rightarrow $ not fuse
Hence in this question option B is correct.
Note:As we see if we want to solve such type of question then we have to find the current which a bulb can bear if the battery gives more current in the circuit if bulb connected in series the current in both bulb is same as current flowing in circuit than in that condition filament of bulb get heat and melt and finally that bulb will be fuse.
Recently Updated Pages
Sets, Relations, and Functions Mock Test 2025-26

NEET Exam Date 2025 and Schedule

Compound Words Sentences Worksheet for Class 4 (Free PDF)

Division Facts Worksheets: Fast Maths Drills for Grades 2-5

Math Drills Division Worksheets | Free Printable PDF Practice

Class 1 Antonyms Worksheet: Printable Opposite Words Practice

Trending doubts
Which are the Top 10 Largest Countries of the World?

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Why is the cell called the structural and functional class 12 biology CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Who discovered the cell and how class 12 biology CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE




