
Answer
377.7k+ views
Hint: Draw a rough diagram of the triangle ABC with the given coordinates and the median AD. Assume the coordinates of A, B and C as $\left( {{x}_{1}},{{y}_{1}} \right)$, $\left( {{x}_{2}},{{y}_{2}} \right)$ and $\left( {{x}_{3}},{{y}_{3}} \right)$ respectively. Now, find the coordinates of the point D by using the midpoint formula given as ${{x}_{D}}=\left( \dfrac{{{x}_{2}}+{{x}_{3}}}{2} \right)$ and ${{y}_{D}}=\left( \dfrac{{{y}_{2}}+{{y}_{3}}}{2} \right)$. Now, consider the ratio 2:3 = m: n and find the coordinates of the point P on the median AD. Use the section formula ${{x}_{P}}=\left( \dfrac{m{{x}_{D}}+n{{x}_{1}}}{m+n} \right)$ and ${{y}_{P}}=\left( \dfrac{m{{y}_{D}}+n{{y}_{1}}}{m+n} \right)$. Find the area of the triangles ABC and PBC using the formulas \[\dfrac{1}{2}\left| \left[ {{x}_{1}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}\left( {{y}_{3}}-{{y}_{1}} \right)+{{x}_{3}}\left( {{y}_{1}}-{{y}_{2}} \right) \right] \right|\] and \[\dfrac{1}{2}\left| \left[ {{x}_{P}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}\left( {{y}_{3}}-{{y}_{P}} \right)+{{x}_{3}}\left( {{y}_{P}}-{{y}_{2}} \right) \right] \right|\] respectively. Take the ratio of area of the triangle PBC and ABC to get the answer. If the area turns out to be negative then take its absolute value.
Complete step by step answer:
Here we have been provided with the coordinates of the vertices A, B and C of a triangle and we are asked to find the ratio of the area of the triangles PBC and ABC when AD is a median and P is a point dividing the median in a certain ratio.
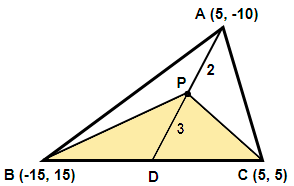
Now, in the above diagram we have considered the coordinates of A, B and C as $\left( {{x}_{1}},{{y}_{1}} \right)$, $\left( {{x}_{2}},{{y}_{2}} \right)$ and $\left( {{x}_{3}},{{y}_{3}} \right)$ respectively. The coordinates of D and P are assumed as $\left( {{x}_{D}},{{y}_{D}} \right)$ and $\left( {{x}_{P}},{{y}_{P}} \right)$ respectively. So we have the values $\left( {{x}_{1}},{{y}_{1}} \right)=\left( 5,-10 \right)$, $\left( {{x}_{2}},{{y}_{2}} \right)=\left( -15,15 \right)$ and $\left( {{x}_{3}},{{y}_{3}} \right)=\left( 5,5 \right)$.
(i) Since AD is the median of the triangle therefore it bisects the side BC of the triangle so using the midpoint formula we get,
For the x – coordinate,
$\begin{align}
& \Rightarrow {{x}_{D}}=\left( \dfrac{{{x}_{2}}+{{x}_{3}}}{2} \right) \\
& \Rightarrow {{x}_{D}}=\left( \dfrac{-15+5}{2} \right) \\
& \Rightarrow {{x}_{D}}=-5 \\
\end{align}$
For the y – coordinate,
$\begin{align}
& \Rightarrow {{y}_{D}}=\left( \dfrac{{{y}_{2}}+{{y}_{3}}}{2} \right) \\
& \Rightarrow {{y}_{D}}=\left( \dfrac{15+5}{2} \right) \\
& \Rightarrow {{y}_{D}}=10 \\
\end{align}$
Therefore the coordinates of D is $\left( -5,10 \right)$.
(ii) Since the point P is present on the median AD such that AP: PD = 2:3, so assuming this ratio as m: n and applying the section formula we get,
For the x coordinate,
$\begin{align}
& \Rightarrow {{x}_{P}}=\left( \dfrac{2\times \left( -5 \right)+3\times \left( 5 \right)}{2+3} \right) \\
& \Rightarrow {{x}_{P}}=\left( \dfrac{-10+15}{5} \right) \\
& \Rightarrow {{x}_{P}}=1 \\
\end{align}$
For the y coordinate,
$\begin{align}
& \Rightarrow {{y}_{P}}=\left( \dfrac{2\times \left( 10 \right)+3\times \left( -10 \right)}{2+3} \right) \\
& \Rightarrow {{y}_{P}}=\left( \dfrac{20-30}{5} \right) \\
& \Rightarrow {{y}_{P}}=-2 \\
\end{align}$
Therefore the coordinates of P is $\left( 1,-2 \right)$.
We know that the area of a triangle with coordinates $\left( {{x}_{1}},{{y}_{1}} \right)$, $\left( {{x}_{2}},{{y}_{2}} \right)$ and $\left( {{x}_{3}},{{y}_{3}} \right)$ is given by the relation \[\dfrac{1}{2}\left| \left[ {{x}_{1}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}\left( {{y}_{3}}-{{y}_{1}} \right)+{{x}_{3}}\left( {{y}_{1}}-{{y}_{2}} \right) \right] \right|\], so we have,
$\Rightarrow $ Area of the triangle ABC = \[\dfrac{1}{2}\left| \left[ 5\left( 15-5 \right)+\left( -15 \right)\left( 5-\left( -10 \right) \right)+5\left( -10-15 \right) \right] \right|\]
$\Rightarrow $ Area of the triangle ABC = 150 square units
Similarly, we can write the area of the triangle PBC as \[\dfrac{1}{2}\left| \left[ {{x}_{P}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}\left( {{y}_{3}}-{{y}_{P}} \right)+{{x}_{3}}\left( {{y}_{P}}-{{y}_{2}} \right) \right] \right|\], so we have,
$\Rightarrow $ Area of the triangle ABC = \[\dfrac{1}{2}\left| \left[ 1\left( 15-5 \right)+\left( -15 \right)\left( 5-\left( -2 \right) \right)+5\left( -2-15 \right) \right] \right|\]
$\Rightarrow $ Area of the triangle ABC = 90 square units
Taking the ratio of areas of the triangles PBC and ABC we get,
$\begin{align}
& \Rightarrow \dfrac{Ar.\left( PBC \right)}{Ar.\left( ABC \right)}=\dfrac{90}{150} \\
& \therefore \dfrac{Ar.\left( PBC \right)}{Ar.\left( ABC \right)}=\dfrac{3}{5} \\
\end{align}$
So, the correct answer is “Option c”.
Note: Here we do not have to apply the Heron’s formula to calculate the area of the triangle as it would require much calculation while finding the length of each side using the distance formula. Also the formula of the area of the triangle given as $\dfrac{1}{2}\times $ base $\times $ height would be suggested not to apply as in this case we need to find the coordinates of the foot of the perpendicular from A and P to the side BC.
Complete step by step answer:
Here we have been provided with the coordinates of the vertices A, B and C of a triangle and we are asked to find the ratio of the area of the triangles PBC and ABC when AD is a median and P is a point dividing the median in a certain ratio.

Now, in the above diagram we have considered the coordinates of A, B and C as $\left( {{x}_{1}},{{y}_{1}} \right)$, $\left( {{x}_{2}},{{y}_{2}} \right)$ and $\left( {{x}_{3}},{{y}_{3}} \right)$ respectively. The coordinates of D and P are assumed as $\left( {{x}_{D}},{{y}_{D}} \right)$ and $\left( {{x}_{P}},{{y}_{P}} \right)$ respectively. So we have the values $\left( {{x}_{1}},{{y}_{1}} \right)=\left( 5,-10 \right)$, $\left( {{x}_{2}},{{y}_{2}} \right)=\left( -15,15 \right)$ and $\left( {{x}_{3}},{{y}_{3}} \right)=\left( 5,5 \right)$.
(i) Since AD is the median of the triangle therefore it bisects the side BC of the triangle so using the midpoint formula we get,
For the x – coordinate,
$\begin{align}
& \Rightarrow {{x}_{D}}=\left( \dfrac{{{x}_{2}}+{{x}_{3}}}{2} \right) \\
& \Rightarrow {{x}_{D}}=\left( \dfrac{-15+5}{2} \right) \\
& \Rightarrow {{x}_{D}}=-5 \\
\end{align}$
For the y – coordinate,
$\begin{align}
& \Rightarrow {{y}_{D}}=\left( \dfrac{{{y}_{2}}+{{y}_{3}}}{2} \right) \\
& \Rightarrow {{y}_{D}}=\left( \dfrac{15+5}{2} \right) \\
& \Rightarrow {{y}_{D}}=10 \\
\end{align}$
Therefore the coordinates of D is $\left( -5,10 \right)$.
(ii) Since the point P is present on the median AD such that AP: PD = 2:3, so assuming this ratio as m: n and applying the section formula we get,
For the x coordinate,
$\begin{align}
& \Rightarrow {{x}_{P}}=\left( \dfrac{2\times \left( -5 \right)+3\times \left( 5 \right)}{2+3} \right) \\
& \Rightarrow {{x}_{P}}=\left( \dfrac{-10+15}{5} \right) \\
& \Rightarrow {{x}_{P}}=1 \\
\end{align}$
For the y coordinate,
$\begin{align}
& \Rightarrow {{y}_{P}}=\left( \dfrac{2\times \left( 10 \right)+3\times \left( -10 \right)}{2+3} \right) \\
& \Rightarrow {{y}_{P}}=\left( \dfrac{20-30}{5} \right) \\
& \Rightarrow {{y}_{P}}=-2 \\
\end{align}$
Therefore the coordinates of P is $\left( 1,-2 \right)$.
We know that the area of a triangle with coordinates $\left( {{x}_{1}},{{y}_{1}} \right)$, $\left( {{x}_{2}},{{y}_{2}} \right)$ and $\left( {{x}_{3}},{{y}_{3}} \right)$ is given by the relation \[\dfrac{1}{2}\left| \left[ {{x}_{1}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}\left( {{y}_{3}}-{{y}_{1}} \right)+{{x}_{3}}\left( {{y}_{1}}-{{y}_{2}} \right) \right] \right|\], so we have,
$\Rightarrow $ Area of the triangle ABC = \[\dfrac{1}{2}\left| \left[ 5\left( 15-5 \right)+\left( -15 \right)\left( 5-\left( -10 \right) \right)+5\left( -10-15 \right) \right] \right|\]
$\Rightarrow $ Area of the triangle ABC = 150 square units
Similarly, we can write the area of the triangle PBC as \[\dfrac{1}{2}\left| \left[ {{x}_{P}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}\left( {{y}_{3}}-{{y}_{P}} \right)+{{x}_{3}}\left( {{y}_{P}}-{{y}_{2}} \right) \right] \right|\], so we have,
$\Rightarrow $ Area of the triangle ABC = \[\dfrac{1}{2}\left| \left[ 1\left( 15-5 \right)+\left( -15 \right)\left( 5-\left( -2 \right) \right)+5\left( -2-15 \right) \right] \right|\]
$\Rightarrow $ Area of the triangle ABC = 90 square units
Taking the ratio of areas of the triangles PBC and ABC we get,
$\begin{align}
& \Rightarrow \dfrac{Ar.\left( PBC \right)}{Ar.\left( ABC \right)}=\dfrac{90}{150} \\
& \therefore \dfrac{Ar.\left( PBC \right)}{Ar.\left( ABC \right)}=\dfrac{3}{5} \\
\end{align}$
So, the correct answer is “Option c”.
Note: Here we do not have to apply the Heron’s formula to calculate the area of the triangle as it would require much calculation while finding the length of each side using the distance formula. Also the formula of the area of the triangle given as $\dfrac{1}{2}\times $ base $\times $ height would be suggested not to apply as in this case we need to find the coordinates of the foot of the perpendicular from A and P to the side BC.
Recently Updated Pages
Who among the following was the religious guru of class 7 social science CBSE

what is the correct chronological order of the following class 10 social science CBSE

Which of the following was not the actual cause for class 10 social science CBSE

Which of the following statements is not correct A class 10 social science CBSE

Which of the following leaders was not present in the class 10 social science CBSE

Garampani Sanctuary is located at A Diphu Assam B Gangtok class 10 social science CBSE

Trending doubts
Write the difference between order and molecularity class 11 maths CBSE

A rainbow has circular shape because A The earth is class 11 physics CBSE

Which are the Top 10 Largest Countries of the World?

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

How do you graph the function fx 4x class 9 maths CBSE

Give 10 examples for herbs , shrubs , climbers , creepers

What are noble gases Why are they also called inert class 11 chemistry CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Differentiate between calcination and roasting class 11 chemistry CBSE



