




How to Use the Speed Formula in Real-Life Maths Problems
A speed formula represents the distance covered at a specific rate. Distance travelled in a given amount of time is the measure of speed. By knowing the distance travelled by an object and the time it took, you can calculate its average speed. The speed formula and its applications will be discussed in this section.
The formula for speed is distance divided by time. The units of speed are meters per second (m/s) or kilometres per hour (km/hr).
Deriving the Formula of Speed
Like any other equation, the speed equation = distance /time can be rearranged.
There are three ways to rearrange the formula:
Distance/time = speed
Speed* time = distance
Distance/speed = time
Two variables are needed to compute one (speed, distance, time).
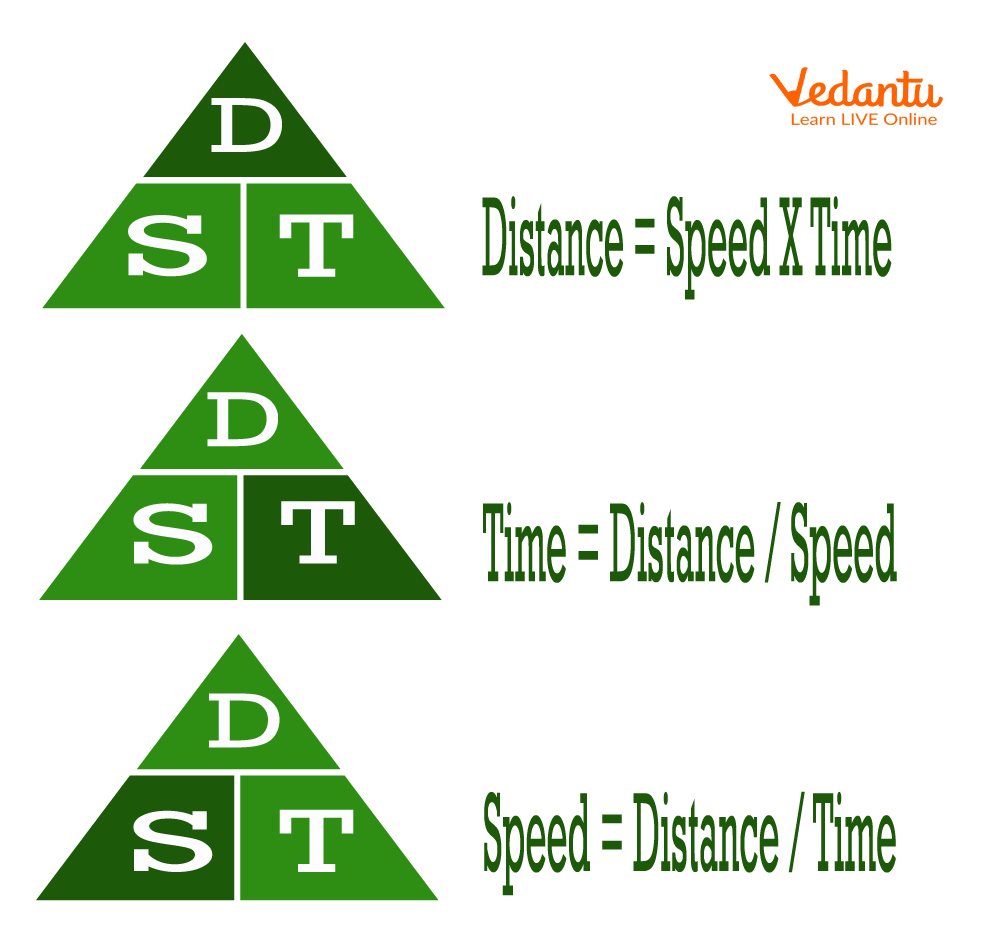
Rearrangement of Formula
In the above-given picture, three different triangles are derived from the formula of speed. In the first triangle, the distance (D) is marked as dark green colour, which means that the formula for distance is given. In the second triangle, the time (T) is marked as dark green, which means that the formula for time is given. In the third triangle, the speed (S) is marked as dark green colour, which means the speed calculation formula can be used to find the speed.
Method for Calculating Average Speed Formula
There is usually a simple formula for calculating the average speed formula.
Speed = $\dfrac{\mathrm{Distance}}{\mathrm{Time}}$
It is possible, however, to use two different speeds for different distances or for different periods of time. It is possible to calculate the average speed using other formulas in these situations. Real-life problems and standardised tests often contain these problems, so learning these formulas and methods is beneficial.
How Does Speed Affect Time and Distance?
Speed involves both distance and time. "Faster" means either "farther" (greater distance) or "sooner" (less time). Doubling one's speed would mean doubling one's distance travelled in a given amount of time. Doubling one's speed would also mean halving the time required to travel a given distance.

Formula in Triangles
Solved Examples
Example 1: What's your speed if you travel 3600 m in 30 minutes?
Ans: Using the speed calculation formula,
Speed = Distance/ Time
$\dfrac{3600}{30 \times 60}$ = 2m/s = speed
Method for Measuring Speed
Most Americans measure speed in miles per hour or mph. In most cases, cars are measured by this method. In Physics, meters per second (m/s) is usually used to calculate speed.
Speed Can be Measured in Two Different Ways:
Instantaneous Speed - The speed of a particular moment. Depending on how quickly the car is driving at this moment, it might slow down or speed up over the next hour.
Distance covered by an object over a given time interval is the basis for calculating the average speed. 50 miles travelled in an hour will result in 50 mph. While the car may have been travelling at instantaneous speeds of 40 mph and 60 mph during that period, its average speed was 50 mph.
Summary
Here we have learnt about the mathematical relation between speed, distance and time. The speed of a moving body is the distance it travels in unit time. A body moving for the same time will travel the same distance.
Distance = speed x time
Speed = distance/ time
To find time, apply the formula for time, t = d/ s, which means time equals distance divided by speed.
If the distance is in km and time is in hours, then the speed is km/hr.
If the distance is in m and the time is in seconds, then the speed is m/sec.
FAQs on Speed Formula: Definition, Examples & Easy Calculations
1. What is the basic formula used for calculating speed?
The basic formula to calculate speed is a fundamental relationship between distance and time. It is expressed as: Speed = Distance / Time. In this formula, 'Speed' is the rate at which an object covers a certain distance, 'Distance' is the total length covered by the object, and 'Time' is the duration it took to cover that distance.
2. A cyclist covers 20 kilometres in 50 minutes. How do you calculate the cyclist's speed in metres per second (m/s)?
To calculate the speed in m/s, you must first convert the given units to metres and seconds. Here is the step-by-step calculation:
- Step 1: Convert Distance: The distance is 20 km. Since 1 km = 1000 metres, the distance in metres is 20 × 1000 = 20,000 m.
- Step 2: Convert Time: The time taken is 50 minutes. Since 1 minute = 60 seconds, the time in seconds is 50 × 60 = 3,000 s.
- Step 3: Apply the Speed Formula: Speed = Distance / Time.
- Step 4: Calculate the Speed: Speed = 20,000 m / 3,000 s = 6.67 m/s.
3. What are the standard units for measuring speed as per the NCERT syllabus?
The standard unit, or SI unit, for measuring speed is metres per second (m/s). However, in many real-world applications, such as vehicle travel, speed is commonly expressed in kilometres per hour (km/h). It's important for students to know how to convert between these units. For example, to convert km/h to m/s, you multiply the value by 5/18.
4. How can the speed formula be rearranged to find the distance or time?
Yes, the speed formula (Speed = Distance / Time) is a versatile equation that can be algebraically rearranged to solve for the other two variables. This is a key skill for solving different types of problems.
- To find Distance: If you know the speed and time, you can find the distance covered by using the formula: Distance = Speed × Time.
- To find Time: If you know the distance and speed, you can find the time taken by using the formula: Time = Distance / Speed.
5. What is the fundamental difference between speed and velocity?
The key difference between speed and velocity lies in the concept of direction.
- Speed is a scalar quantity, which means it only has magnitude (a numerical value). For example, 60 km/h.
- Velocity is a vector quantity, which means it has both magnitude and a specified direction. For example, 60 km/h towards the North.
6. How do you calculate the average speed of a journey with varying speeds?
To find the average speed for an entire journey where speeds vary, you should not simply average the different speeds. The correct method is to use the formula: Average Speed = Total Distance Covered / Total Time Taken. You must first calculate the total distance of the entire journey and divide it by the total time spent travelling, including any periods at different speeds.
7. In what ways is the formula for speed used in our daily lives?
The concept of speed is applied constantly in everyday situations. For instance:
- Travel: We use it to estimate the time it will take to reach a destination by car, train, or plane.
- Driving: A car's speedometer shows its speed, helping drivers adhere to speed limits for safety.
- Sports: We measure the speed of a running athlete or a thrown ball to analyse performance.
- Technology: The speed of an internet connection is measured in Mbps (megabits per second), which is an application of the speed formula.
8. Does a car's speedometer display average speed or instantaneous speed?
A car's speedometer displays its instantaneous speed. This is the speed of the vehicle at that precise moment in time. It can change from one second to the next as you accelerate or brake. Average speed, in contrast, would be calculated after the trip is over by dividing the total distance travelled by the total time the journey took, which is a different value.





















