Step-by-Step Guide to Solving for the Missing Leg in Right Triangles
According to the Pythagoras theorem, the square of the hypotenuse equals the sum of the squares of the remaining two sides in a right-angled triangle.
Let's solve some questions for further understanding -
Questions:
Find the value of y in the given triangle.
Image - an image of a triangle
Identify the length of the hypotenuse?
Image - an image of a triangle
What is the value of the missing side of the triangle?
Image - an image of a triangle
Find the value of x.
Image - an image of a triangle
Find the value of c.
Image - an image of a triangle
Find the value of the missing side.
Image - an image of a triangle
In a right triangle, the longest side is 8 cm. One of the remaining sides is 4√3 cm long. Find the length of the other side.
Use Pythagoras Theorem to find the missing side.
Image - an image of a triangle
Find the third side of the given triangle.
Image - an image of a triangle
Is ∆ABC a right angled triangle, where AB = 5cm, BC = 10cm, AC = 15cm?
What is the length of the hypotenuse in the given triangle?
Image - an image of a triangle
Find the missing side by using Pythagoras Theorem.
Image - an image of a triangle
What is the length of the hypotenuse of the given triangle ?
Image - an image of a triangle
ABC is a right triangle. AC is its hypotenuse. Length of side AB is 2√5. Side BC is twice of side AB. Find the length of AC.
Find the length of the hypotenuse.
Image - an image of a triangle
Answers -
By Pythagoras theorem, we get
z2=x2+y2
Now, directly substituting the values
⇒ 169 = 25 + y2
⇒ y2 = 144 ⇒ y = 12
Hence, the value of y is 12.
5.1mm
By Pythagoras Theorem, a2+b2=c2
Let a=3 b= 6
9 + 36 = c2 ⇒ 45 = c2
√45 = c
By the Pythagoras Theorem, Hypotenuse2 = Base2 + Perpendicular2
x2 = 64+36 = 100
x = 10
Therefore, the value of x is 10.
By Pythagoras Theorem, a2+b2=c2
Let a=5 b=7
25 + 49 = c2 ⇒ 74 = c2
√74 = c
Therefore, the value of c is √74.
By Pythagoras Theorem, a2+b2=c2
Let a=5 b=5
25 + 25 =c2 ⇒ 50 = c2
√50 = c
4cm.
By Pythagoras Theorem, a2+b2=c2
Let c =19 b=17
a2 + 289 = 361 ⇒ 72 = a2
√72 = a
Given: a = 3, c = 5
Putting the values in the Pythagoras Formula: a2+b2=c2
9 + b2 = 25
b2 = 25 − 9 = 16
b = 4
Therefore, the third side is 4.
If ∆ABC is a right angled triangle, then AB2+BC2=AC2
AB = 5, BC =10, AC = 15
AB2 + BC2 = 25 + 100 = 125
AC2 = 225
Since, AC2 ≠ AB2 + BC2
Hence, ABC is not a right-angled triangle.
9.6m.
By Pythagoras Theorem, a2+b2=c2
Let c =20 b=10
a2 + 100 = 400 ⇒ 300 = a2
√300 = a
Pythagoras Formula: a2+b2=c2
Let AB = a = 20, BC = b = 21
Putting values in the formula
400 + 441 = c2
841 = c2
c = 29 cm
AC = 10
10in
Importance of Geometry Pythagorean Theorem Worksheet for Class KG-3
The students of KG-3 need to complete their syllabus to score good marks in the examinations. The chapter on the Pythagorean theorem is important; students need to complete the chapter to complete their syllabus. The experts of Vedantu have formulated worksheets filled with important questions based on the topic. Solving the questions from Geometry Pythagorean Theorem Worksheet will enable the students to find solutions to some of the challenging questions in the chapter, further cementing their knowledge.
There are different questions related to finding the missing side of the triangle in this worksheet, and students can find the right approach to solve these questions easily. That is one of the main reasons the worksheets are considered to be some of the most important study materials they need to include in their study routine. Download Find The Missing Side of a Triangle Worksheet from Vedantu and get all the chapter details from there.
Benefits of Find Missing Side of Each Triangle Worksheet for Kids
There are many benefits of downloading the Pythagorean Theorem worksheet for children of Class KG-3. Here we have provided some of the main benefits students can have from the worksheets.
Find the Missing Side of Each Triangle Worksheet has been provided by Vedantu’s Maths expert. Thus, the questions in the worksheet will ensure that students have no trouble understanding the concept.
They can download the solutions and practice the questions regularly to prepare for their exams. These worksheets will also help them revise the topic easily.
The experts at Vedantu have solved all the questions to provide easy reference to the students. KG-3 students can refer to these solutions to clarify any doubts that they might have about the chapter.
The experts have also explained the methods for solving the questions and provided some simple tips to help the students get a good understanding. Thus, students can download the study material and boost their preparation easily.
Learn Pythagoras Theorem Properly With Helpful Worksheets
Students can easily download the Pythagorean Theorem Find The Missing Leg Worksheet from Vedantu. These study materials are free of cost and will ensure that students have all the important study materials needed to complete the chapter in time. The questions and solutions have been provided to complete the syllabus of students and aid them in their exam preparation. This is your chance to download the worksheets and ensure you are fully prepared to score good marks.
FAQs on Find the Missing Leg: Pythagorean Theorem Worksheet for Students
1. What is the Pythagorean theorem and what is its main purpose in Maths?
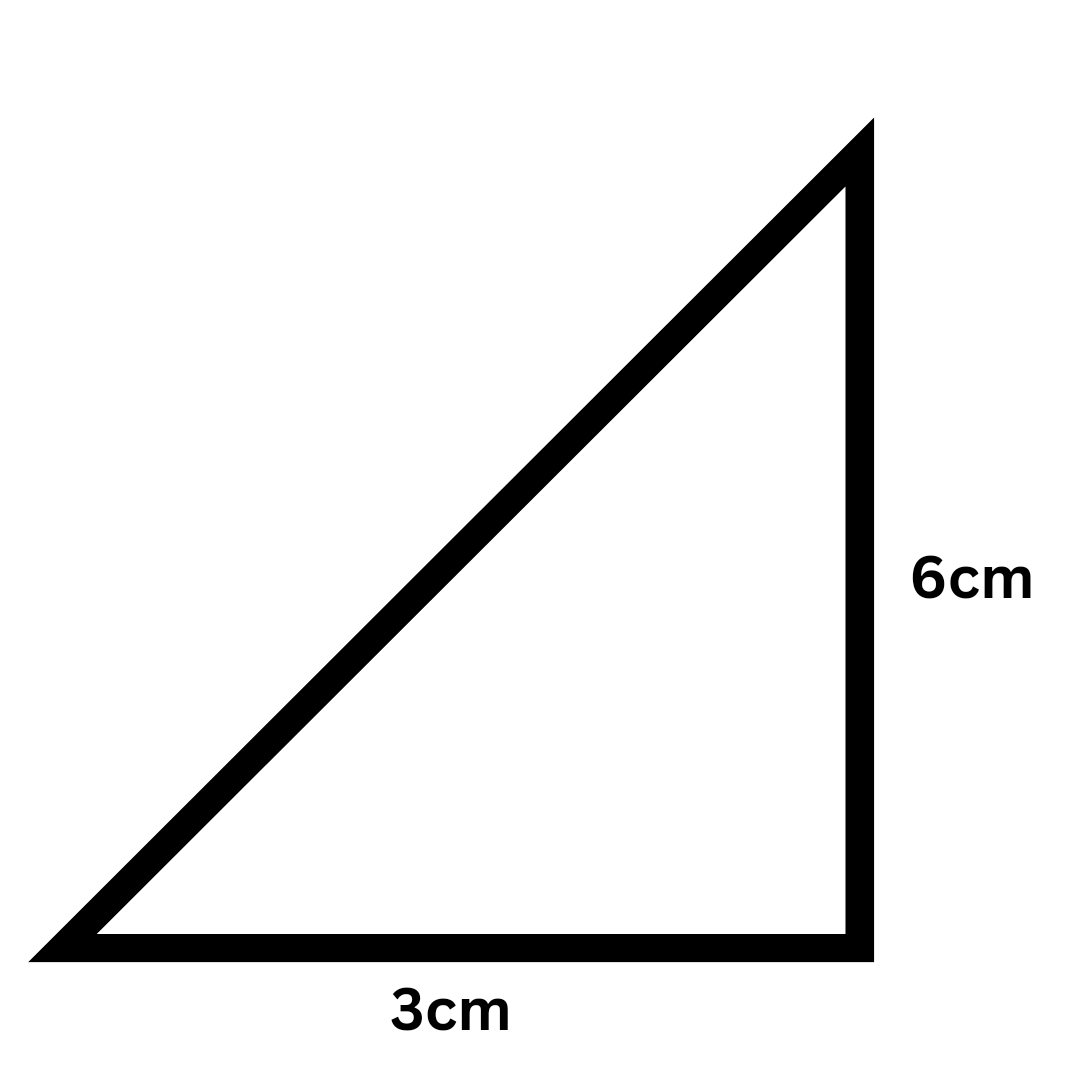
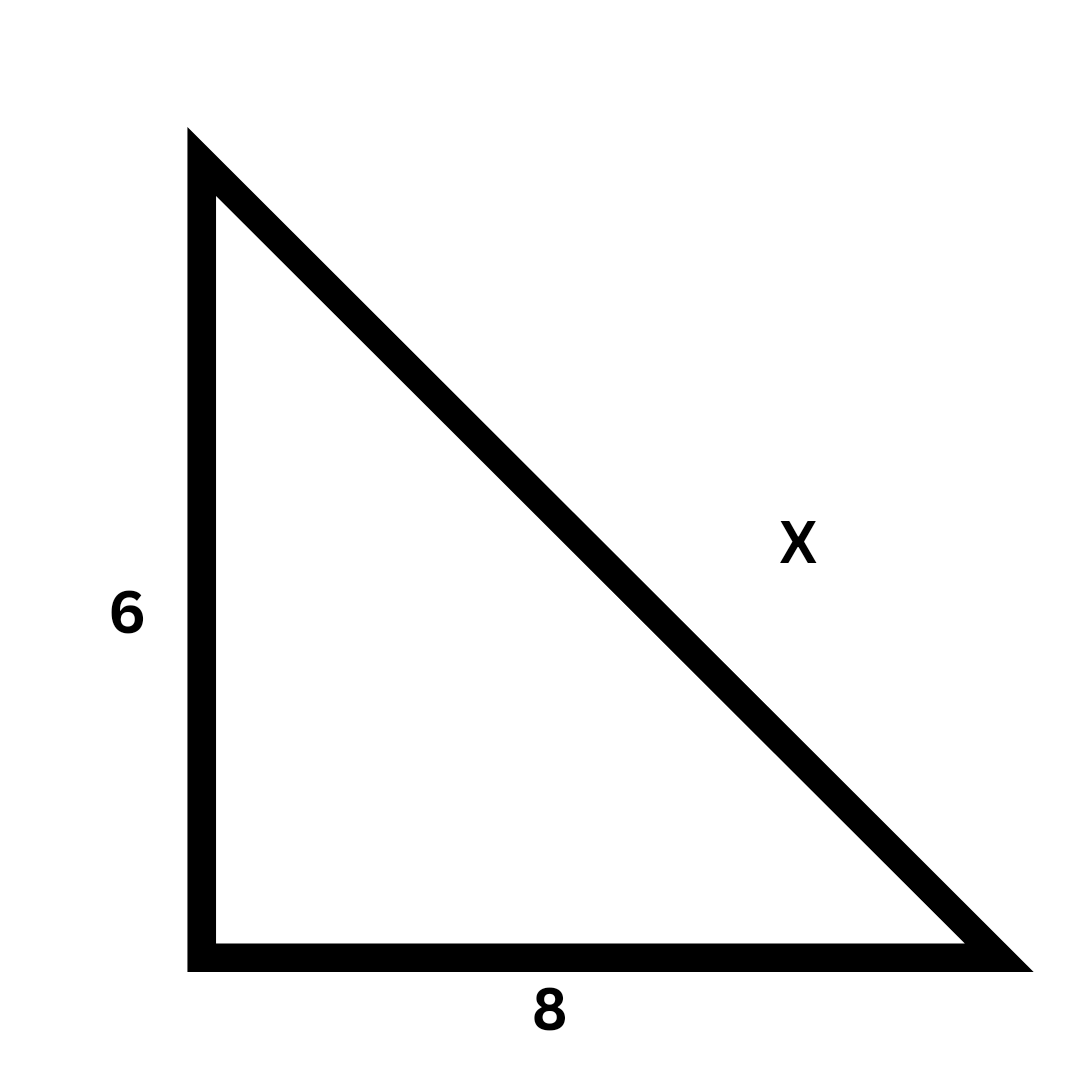
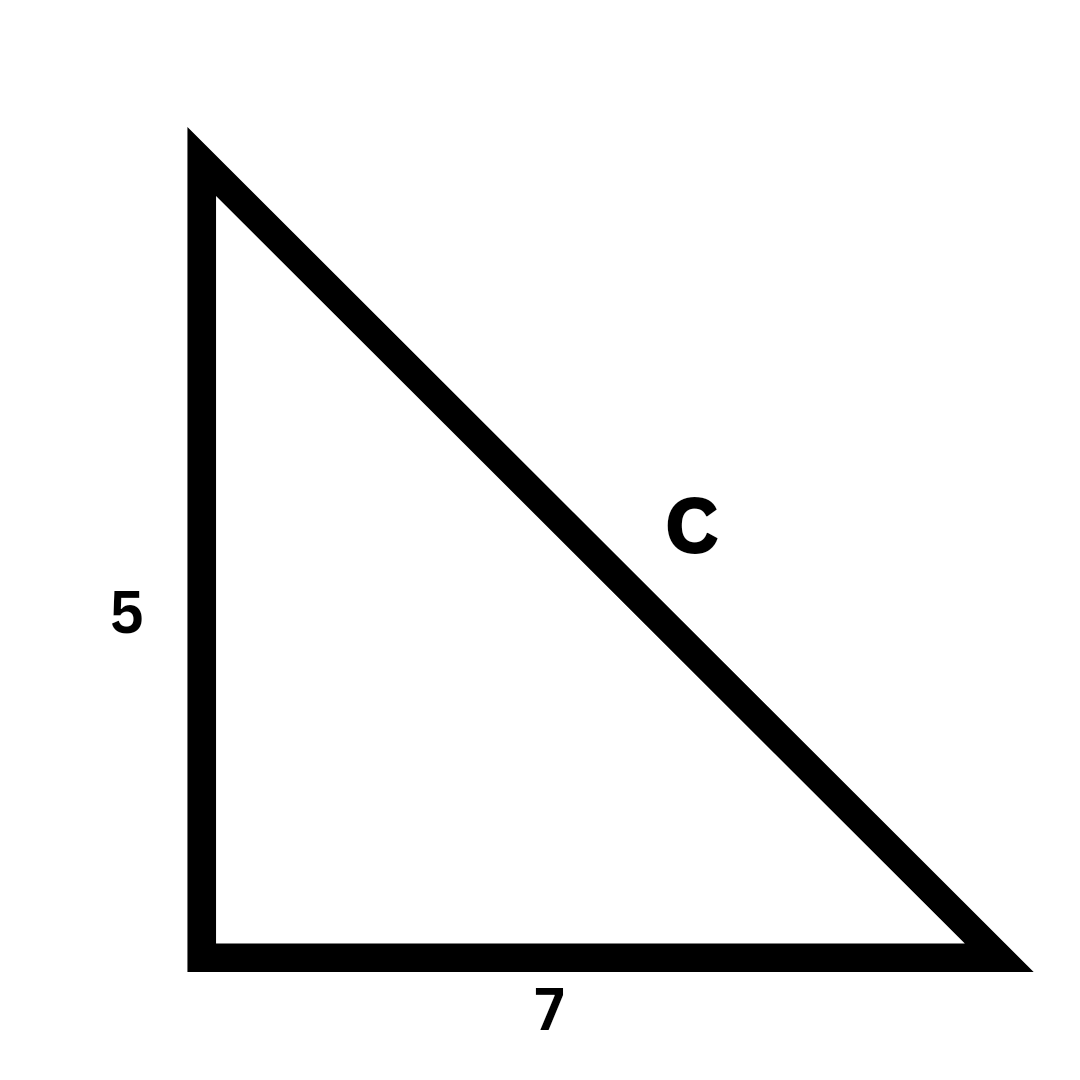
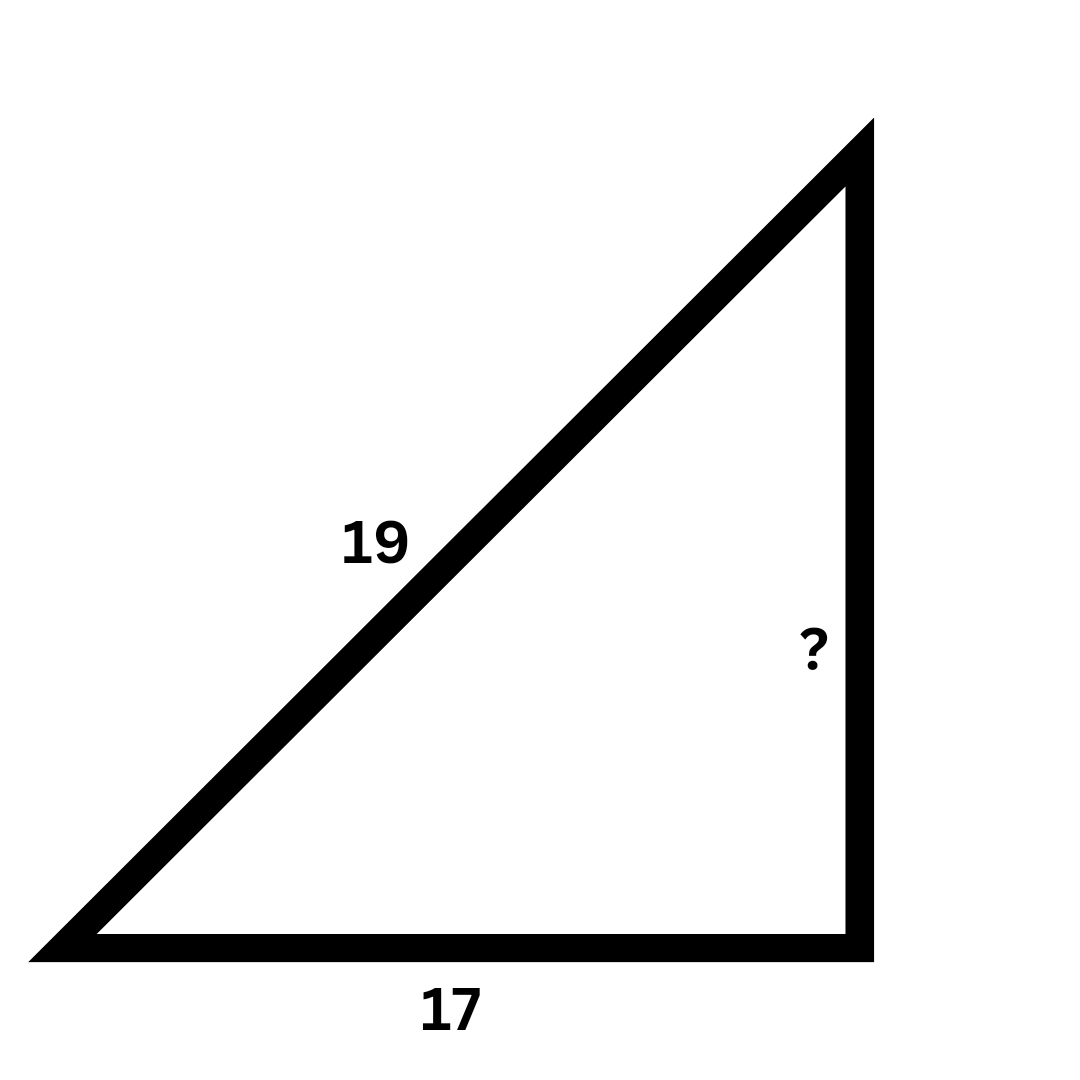
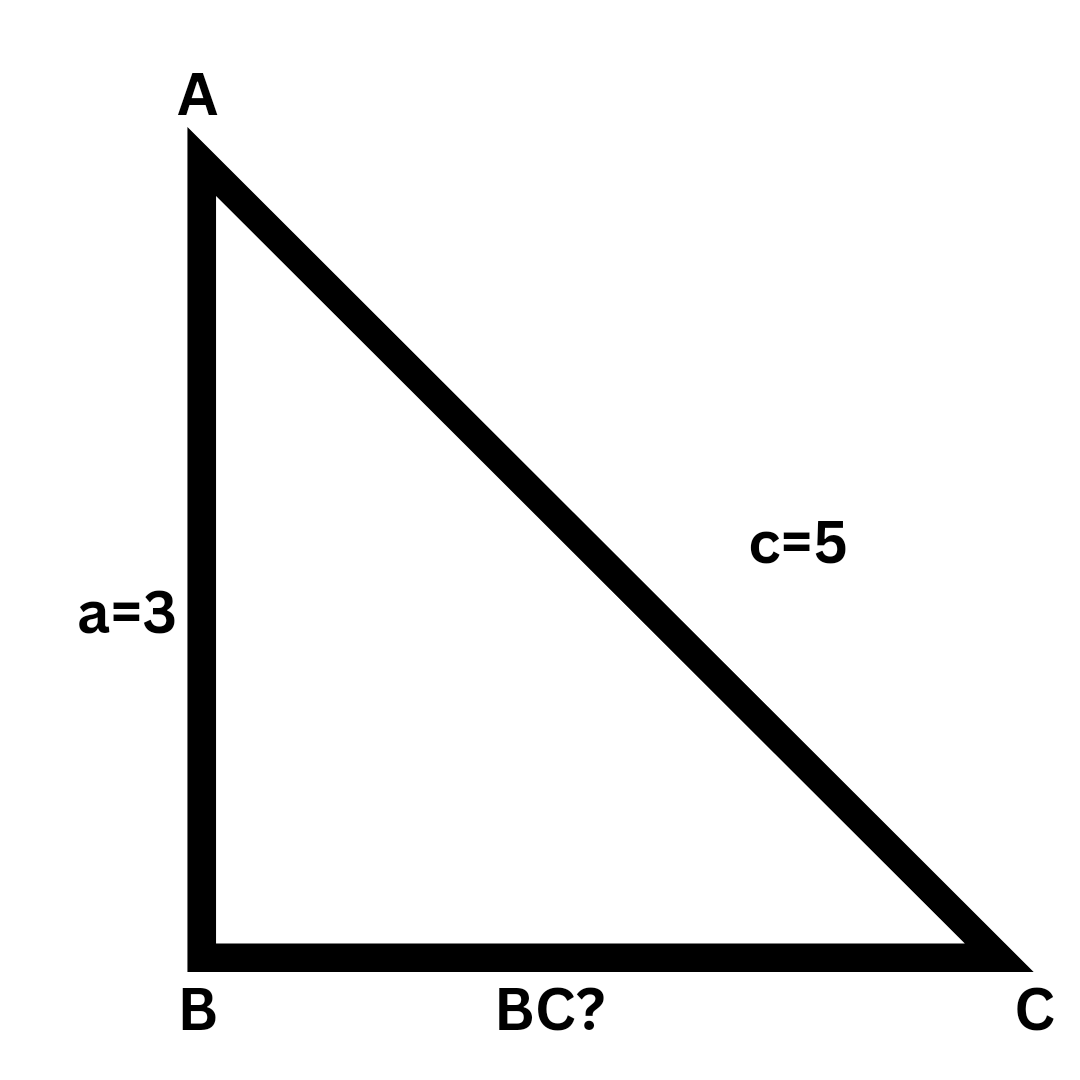
The Pythagorean theorem is a fundamental principle in geometry that states that in a right-angled triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides (legs). Its main purpose is to find the length of a missing side when the lengths of the other two sides are known, using the formula a² + b² = c².
2. How do you identify the 'legs' and the 'hypotenuse' in a right-angled triangle?
In any right-angled triangle, the hypotenuse is always the longest side and is located directly opposite the 90-degree angle. The other two sides, which form the right angle, are called the legs. Correctly identifying these parts is the first crucial step before applying the Pythagorean theorem to find a missing side.
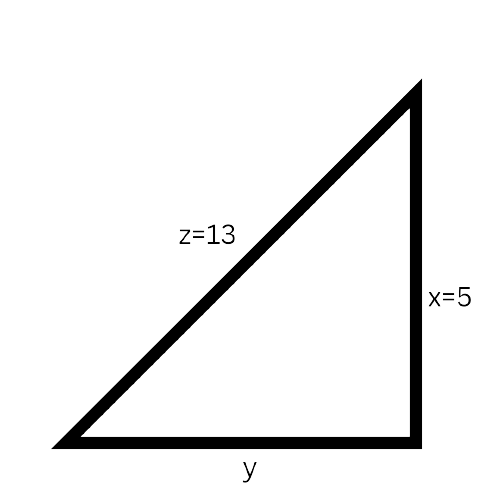
3. What is the specific formula used to find a missing leg of a right-angled triangle?
To find a missing leg (for example, side 'a'), you must rearrange the standard Pythagorean formula. The correct formula is a² = c² - b². This means you subtract the square of the known leg ('b') from the square of the hypotenuse ('c'). Afterwards, you calculate the square root of the result to determine the length of the missing leg 'a'.
4. Why is it impossible for a leg of a right-angled triangle to be longer than the hypotenuse?
It is mathematically impossible because the hypotenuse is, by definition, the side opposite the largest angle (90°) in a right-angled triangle, which makes it the longest side. According to the formula c² = a² + b², the square of the hypotenuse is the sum of the squares of the two legs. Therefore, the value of 'c' must always be greater than both 'a' and 'b' individually.
5. What is the most common mistake students make when trying to find a missing leg?
The most common mistake is incorrectly adding the squares of the sides instead of subtracting. When solving for a leg (side 'a' or 'b'), you must subtract the square of the known leg from the square of the hypotenuse (e.g., a² = c² - b²). Accidentally using addition (a² = c² + b²) is a frequent error that leads to an incorrect answer.
6. Can you use the Pythagorean theorem for triangles that are not right-angled?
No, the Pythagorean theorem is a special property that applies exclusively to right-angled triangles. The entire relationship described by a² + b² = c² is dependent on one angle being exactly 90 degrees. Using this formula for acute or obtuse triangles will not produce correct side length measurements.
7. How does practising with a worksheet improve understanding of the Pythagorean theorem?
Practising with a dedicated worksheet helps solidify the concept in several ways:
It trains you to quickly and accurately identify the legs and hypotenuse in different orientations.
It provides essential practice in correctly rearranging the formula to solve for a leg versus the hypotenuse.
It builds confidence and speed in performing the required calculations involving squares and square roots.
8. What are some real-world examples where you would need to find the missing leg of a right triangle?
You can apply this concept in many practical situations. For instance:
A carpenter knows the length of a diagonal support beam (hypotenuse) and the width of a frame (one leg). They can calculate the required height of the frame (the other leg).
To find how high a ladder reaches on a wall, if you know the ladder's length (hypotenuse) and the distance of its base from the wall (one leg).
