




Explore Definitions and Real-Life Examples of Maths Words Starting with E
Maths is one of the unique languages of science that deals with numbers and builds logical thinking and analytical reasoning skills. So, Maths vocabulary plays a very crucial role in understanding the Maths concepts better and developing Maths skills. Many times, we see that students are unable to process or make sense of what they are doing. If a student is unable to develop a Maths concept fully, then it will lead to a misconception and lack of understanding of the next skills because this is a building-block process. Therefore, students should have these foundational building blocks to advance to higher levels.
So, in this article, we will introduce you to the list of Mathematical words or terms that start with the letter ‘e’ which will help you to boost your Mathematical vocabulary skills.
List of Mathematical Words Starting with the Letter ‘E’
In this section, we have explained some of the Mathematical terms that start with ‘e’ in detail with examples. So, try to explore all the words and save as much as possible in your vocabulary bank.
Edge
In Geometry, an edge is a line segment that joins one vertex to another.
Example: A cube has 12 edges.
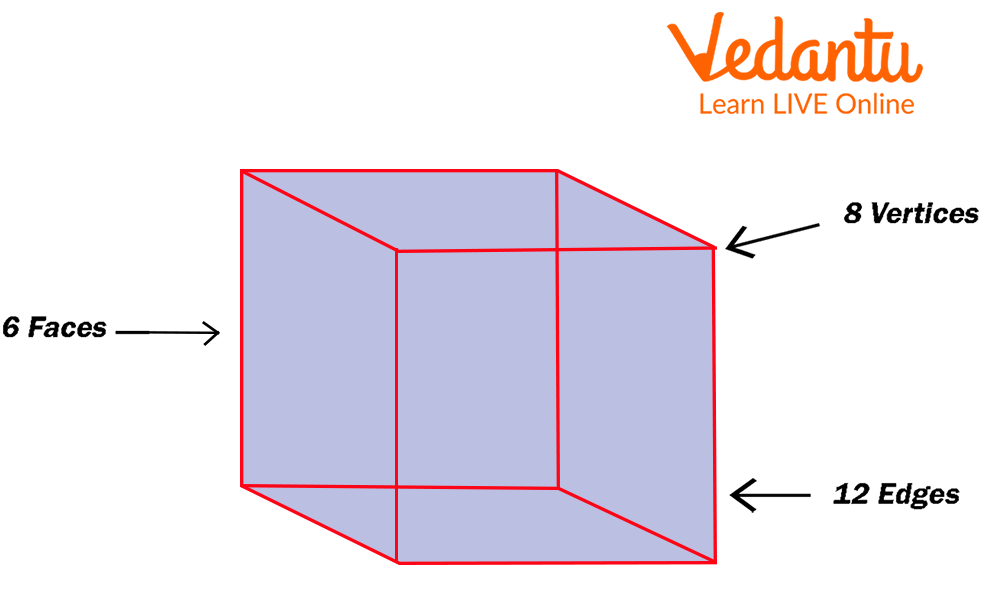
Cube
Endpoints
In Geometry, the points on either end of a line segment or one end of a ray are called endpoints.
Example:

Endpoints
Even Numbers
An even number is a number that can be divisible by 2 and after dividing even numbers by 2, we get 0 as a remainder. So, we can say that the numbers ending with 0, 2, 4, 6, and 8 are even numbers.
Example:
Equilateral Triangle
In Geometry, an equilateral triangle is a triangle that is composed of three sides equal in length and all the angles are equal in measure in an equilateral triangle.
Example:
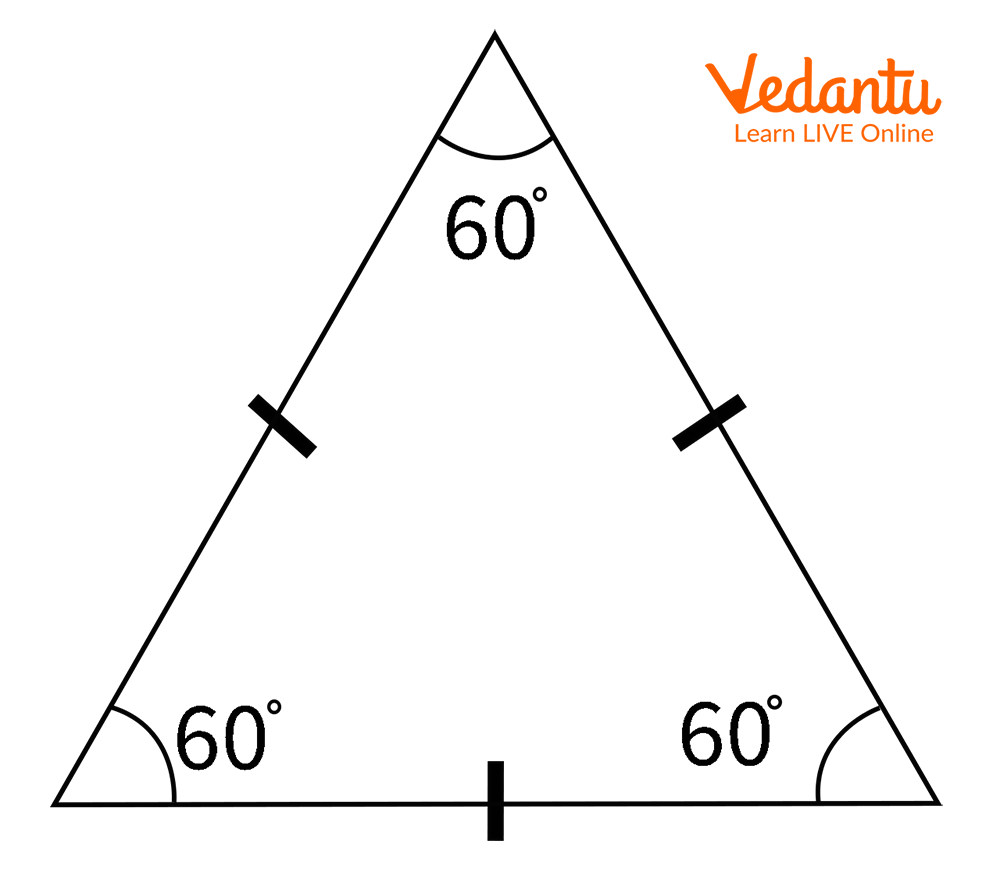
Equilateral Triangle
Equivalent Fractions
In Mathematics, equivalent fractions can be defined as the fractions that might have different denominators and numerators but are equal to the same value. All equivalent fractions result in the same fraction in their simplest form.
Example: 1/4, 2/8, 4/16, 8/32 — all the fractions represent the same value that is 1/4. So, all these are equivalent fractions.
Equation
In Maths, an equation is defined as a Mathematical statement that is composed of two algebraic expressions with the same value connected by an equal sign.
The algebraic expressions in Maths can have one or more than one variable.
Example: 5x + 10y = 20 is an equation where 5x + 10y and 20 are two expressions, connecting by an equal sign.
Element of a Set
All the objects or items present in a set are called elements. All the elements in a set are separated by commas and enclosed by curly brackets.
Example: A={2, 4, 6, 8, 10} is a set where 2, 4, 6, 8, 10 are the elements of the set A.
Empty Set
An empty set can be defined as a set that has no elements. It is also called a null set and is represented as {} or it can also be represented by using the symbol '∅'.
Exponent
An exponent can be defined as a number that tells you how many times a number is multiplied by itself. Exponent is also represented as the power of a number.
Example: 4×4×4 is the expanded form of 43 where 4 is multiplied by itself three times. Here, ‘3’ is called the exponent or power and ‘4’ is called the base.
Expanded Form
Expanded form is a way of showing up a number as a sum of each digit multiplied by its place value.
Example: 7892 can be expanded as 7000+800+90+2.
Conclusion
In this article, we have covered the most important Mathematical terms with examples which start with the letter ‘e’. Students need to practise and learn these concepts so that they don’t face any difficulties while solving problems at higher levels.
FAQs on Essential Maths Glossary: Words Starting with E
1. What are some important mathematical terms that start with the letter E?
Several key mathematical terms start with E, covering different areas of maths. The most common ones as per the CBSE syllabus include:
- Equation: A statement that asserts the equality of two mathematical expressions, always containing an equals sign (=).
- Expression: A combination of numbers, variables, and operators that represents a value but does not have an equals sign.
- Even Number: An integer that is exactly divisible by 2, with no remainder.
- Estimate: An approximate calculation or judgment of a value, number, or quantity.
- Edge: A line segment where two faces of a three-dimensional shape meet.
- Exponent: A number that indicates how many times a base number is to be multiplied by itself.
- Element: A single object or member belonging to a set.
2. What is the main difference between an 'equation' and an 'expression' in algebra?
The key difference lies in the presence of an equals sign (=). An expression is a standalone mathematical phrase (e.g., 5x + 2), which can be simplified or evaluated. An equation, however, is a complete mathematical sentence stating that two expressions are equal (e.g., 5x + 2 = 12). Essentially, you solve an equation to find the value of a variable, whereas you simplify an expression.
3. How is the concept of an 'edge' used to describe 3D shapes in geometry?
In geometry, an edge is a fundamental component used to define the structure of a three-dimensional (3D) shape, also known as a polyhedron. It is the straight line segment formed where two flat faces of the shape intersect. For example, a cube is defined by its 12 edges, 6 faces, and 8 vertices. Understanding edges is crucial for applying formulas like Euler's formula (F + V - E = 2).
4. What does it mean to 'estimate' a value in maths, and can you give an example?
To estimate in maths means to find a value that is close enough to the right answer, usually by making the numbers simpler through rounding. It is a useful skill for checking if an answer is reasonable. For example, to estimate the product of 19 and 22, you could round 19 to 20 and 22 to 20. The estimated product would be 20 × 20 = 400, which is close to the exact answer of 418.
5. How is estimation used in real-life situations outside the classroom?
Estimation is a practical skill used constantly in everyday life for making quick decisions. For instance, you might:
- Estimate the total bill at a grocery store to ensure you have enough money.
- Estimate the travel time for a journey based on distance and average speed.
- Estimate the amount of ingredients needed when cooking for a different number of people than a recipe states.
- Estimate the amount of paint required to cover a wall in a room.
6. What is the definition of an 'even number' with examples?
An even number is any integer that can be perfectly divided by 2, leaving no remainder. A simple way to identify an even number is to check its last digit. If the number ends in 0, 2, 4, 6, or 8, it is an even number. Examples include 16, 38, 94, and 250.
7. What is an 'exponent' and what is its main purpose in mathematics?
An exponent is a number that indicates how many times its base number should be multiplied by itself. It is written as a small number to the upper right of the base. For example, in the term 7³, the base is 7 and the exponent is 3. Its main purpose is to provide a compact way to write repeated multiplications (7 × 7 × 7) and to simplify calculations involving very large or very small numbers, which is fundamental in scientific notation.















