




Quick Guide: Definitions and Examples of Common Fraction Terms
We know that fraction is part of something which is whole. This whole can be any object or number. Hence in general we can say that fraction is a small portion or part of any item. In the same way in terms of numbers, it is part of a whole number. There are a lot of terminologies are related to fractions which are often used in mathematics. These words come under fraction vocabulary. Some of the important words of fraction vocabulary are discussed below with their meanings.
List of Words
A list of words of fraction vocabulary with their meaning are given below. You can use these words while writing or talking about fractions.
Let’s understand the meaning of these terms in detail.
Fraction – A fraction is a part of a collection, set or a whole.
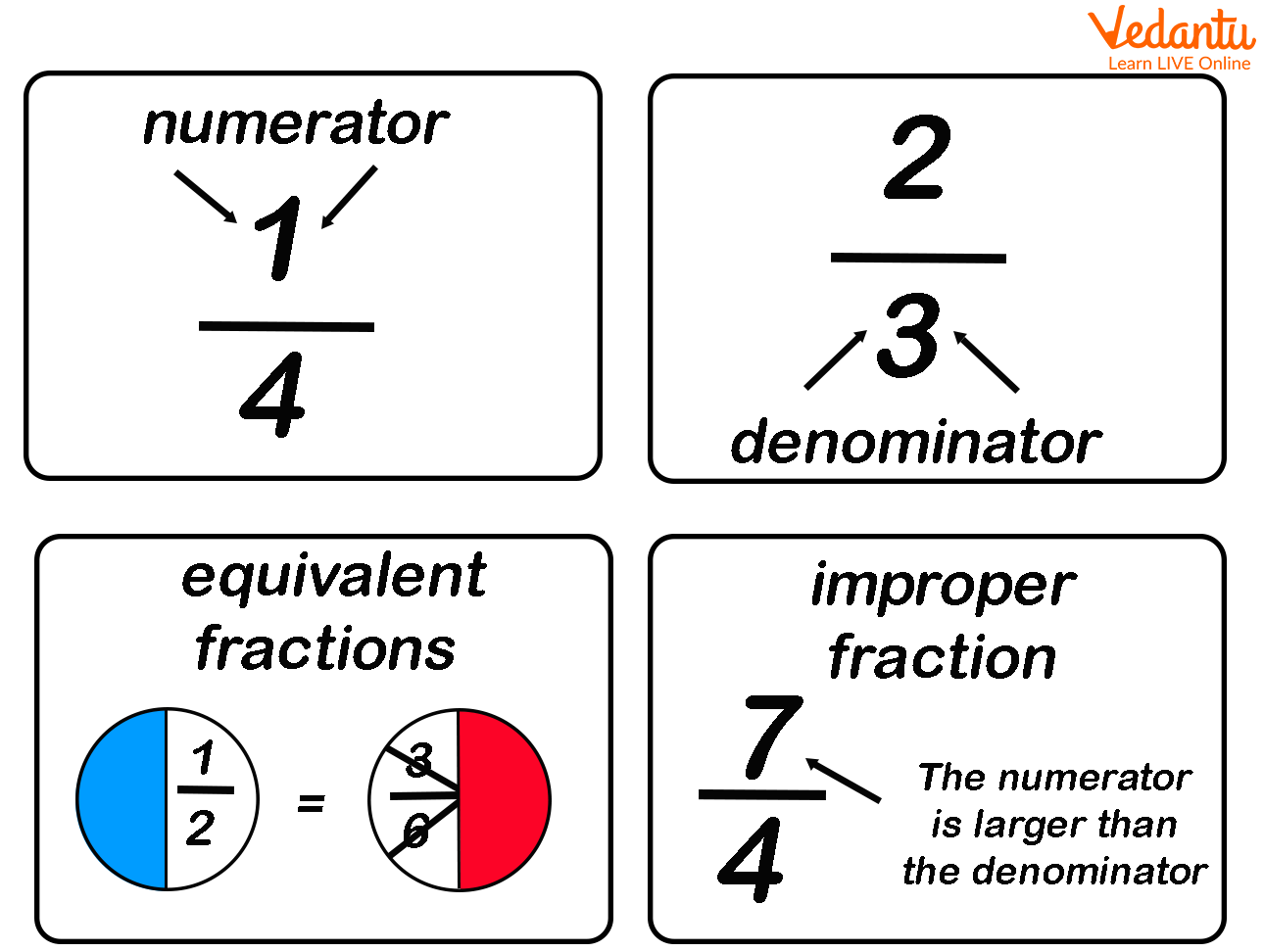
Numerator – Numerator is the number or digits placed above the bar in a fraction, it represents how many equal parts of the whole are indicated.
Denominator – Denominator is the number or digits placed below the bar in a fraction. It represents how many equal parts are present in the whole.
Fraction Vocabulary
Proper fraction – A proper fraction is a type of fraction where the numerator is less than the denominator, less than a whole
Improper fraction – An improper fraction is a type fraction where the numerator is greater than the denominator, greater than a whole
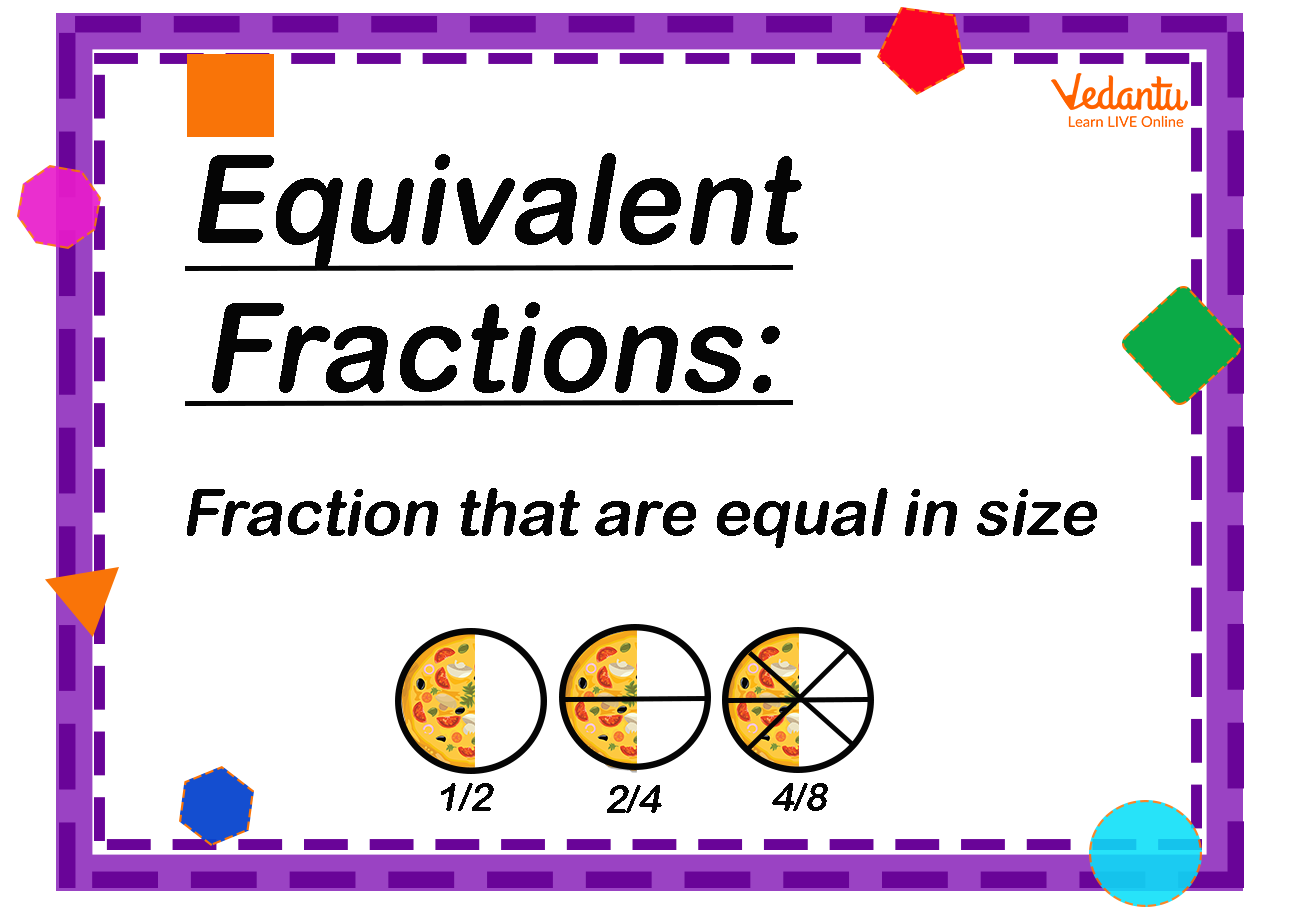
Equivalent fraction – Equivalent fraction is fractions that give equal fraction values. Hence equivalent fractions that name the same amount.
Equivalent Fractions
Simplest terms – The simplest term is a fraction where the numerator number and the denominator have no common factors except 1. Hence the number 1 is the only common factor in such type of traction. For example, \[ \frac{2}{3} \] is the simplest term because there is no common factor except 1.
Mixed Number – A mixed number is consist of two parts. These are; a whole number and a fraction. For example 5 \[ \frac{1}{4} \] . Here 5 is the whole number while \[ \frac{1}{4} \] is a fractions. So this is a mixed number.
Half of- Half of is equal to\[ \frac{1}{2} \] .

Half of
A quarter of- Quarter of is equal to \[ \frac{1}{4} \] .
Conclusion
The above article explains some words of fraction vocabulary. These words are important for us to understand the concept of fractions. When we will go to the higher class it is important to clear the concept and terminologies of the previous class and this article will help students in doing so.
FAQs on Fraction Vocabulary: Essential Terms & Complete Word List
1. What are the essential vocabulary words for understanding fractions?
To understand fractions properly, you must know these key terms:
- Numerator: The top number in a fraction, which shows how many parts of the whole are being considered.
- Denominator: The bottom number in a fraction, which shows the total number of equal parts the whole is divided into.
- Proper Fraction: A fraction where the numerator is smaller than the denominator (e.g., 2/5). Its value is always less than 1.
- Improper Fraction: A fraction where the numerator is greater than or equal to the denominator (e.g., 8/5). Its value is 1 or more.
- Mixed Number: A number that combines a whole number and a proper fraction (e.g., 1 3/5).
- Equivalent Fractions: Fractions that represent the same value, even though they have different numerators and denominators (e.g., 1/2 and 4/8).
- Simplest Terms: A fraction is in its simplest terms when its numerator and denominator have no common factors other than 1.
2. Why is it important to know the difference between a numerator and a denominator?
Understanding the difference is fundamental to grasping what a fraction represents. The denominator tells you the 'size' of the slices (e.g., a denominator of 8 means a pizza is cut into 8 equal slices), setting the context for the whole. The numerator tells you the 'quantity' of those slices you have (e.g., a numerator of 3 means you have 3 of those 8 slices). Without knowing the role of each, you cannot accurately compare fractions or understand their true value.
3. What is the main difference between a proper fraction, an improper fraction, and a mixed number?
The main difference lies in their value relative to a whole number. A proper fraction, like 3/4, is always less than one whole because the numerator is smaller than the denominator. An improper fraction, like 7/4, is equal to or greater than one whole because the numerator is larger than the denominator. A mixed number, like 1 3/4, explicitly shows this by combining a whole number with a proper fraction.
4. Can an improper fraction also be written as a mixed number? How are they related?
Yes, any improper fraction can be converted into a mixed number. They are two different ways of expressing the same value that is greater than one. To convert an improper fraction like 11/4, you divide the numerator (11) by the denominator (4). The result is 2 with a remainder of 3. The quotient (2) becomes the whole number, the remainder (3) becomes the new numerator, and the denominator (4) stays the same. Thus, 11/4 is the same as the mixed number 2 3/4.
5. What does it mean for a fraction to be in its 'simplest terms'?
A fraction is in its simplest terms (or lowest terms) when you cannot divide both the numerator and denominator by any common whole number other than 1. For example, the fraction 6/8 is not in its simplest terms because both 6 and 8 can be divided by 2. After dividing, you get 3/4, which is the simplest form of 6/8 because 3 and 4 share no common factors besides 1.
6. How are the concepts of 'equivalent fractions' and 'simplifying fractions' connected?
They are closely related concepts involving the same principle. Equivalent fractions are fractions that have the same value, such as 1/2, 2/4, and 5/10. Simplifying a fraction is the process of finding its simplest equivalent fraction. For example, when you simplify 5/10, you are finding the equivalent fraction that uses the smallest possible whole numbers, which is 1/2. So, simplifying is a specific type of process to find the most basic form among a set of equivalent fractions.
7. Besides cooking, what are some other real-world examples where we use fraction vocabulary?
Fraction vocabulary is used in many daily situations. For instance:
- Telling Time: We talk about a 'quarter past' an hour or a 'half-hour'.
- Shopping: Sales and discounts are often in fractions, such as 'half off' or 'a third of the original price'.
- Measurements: Carpenters and engineers measure objects using mixed numbers, like '2 and a half inches'.
- Sharing: When you share a chocolate bar with two friends, you each get one-third of the bar.









