How to Apply Divisor, Dividend, Quotient, and Remainder in Problems
The dividend-quotient formula shows the relationship between the dividend, the divisor, the quotient and the remainder, which is one of the main aspects of division. Division is the process of dividing a number into equal parts, leaving a remainder if the number cannot be further divided. The quotient formula of the remainder of division is an important rule in division. Let us learn more about these concepts ahead!
Parts of a Division
What Is the Divisor Dividend Quotient Remainder?
Divisor
A divisor is a number that divides the other number in the calculation. The divisor definition states that it is the term performing the division operation on the dividend. For example, when we divide the number 28 by the number 7, 7 is called the divisor, whereas the number 28 is called the dividend.
The formula for Divisor = (Dividend - remainder) ÷ Quotient
Dividend
A dividend is a whole number or the number of things that need to be divided into certain equal parts. Dividend is the number that is to be divided by the divisor.
The formula for Dividend = Divisor x Quotient + Remainder
Quotient
When you divide two numbers, the result of their division, called a quotient, will be a whole number. If the two numbers have no remainder when divided, they are called "perfect" factors and their quotient is their "product".
The formula for Quotient = Dividend ÷ Divisor.
Remainder
In Mathematics, the remainder is the amount "left over" after performing some computation. In arithmetic, the remainder is the integer "left over" after dividing one integer by another to produce an integer quotient.
The formula for Remainder = dividend - (divisor × quotient)
For example, 75 divided by 9 gives 8 as a quotient and 3 as a remainder.
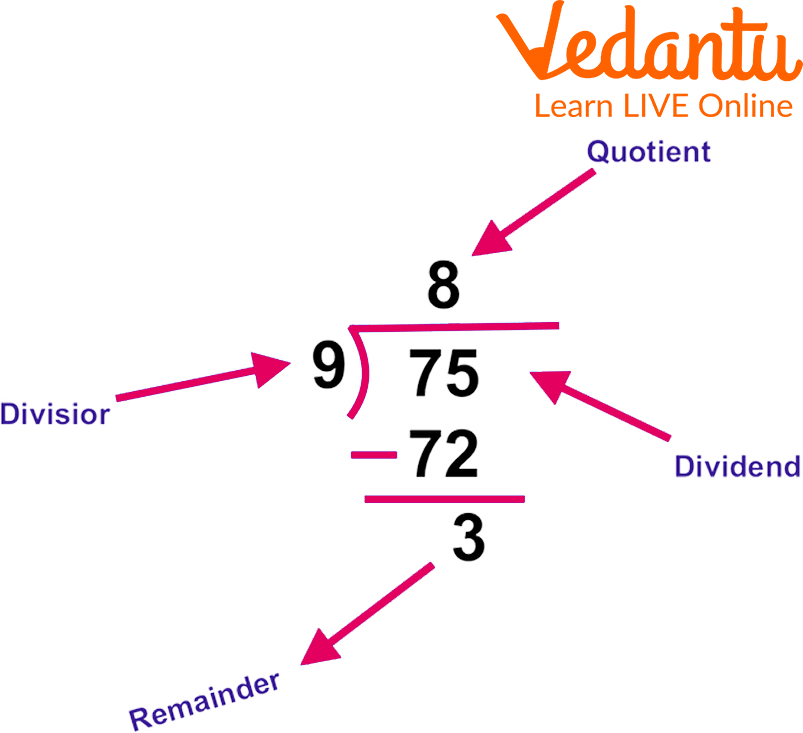
Divisor Dividend Quotient and Remainder
Where Are Dividend, Divisor, Quotient and Remainder Used in Maths?
The divisor is used in the decimal system to convert a decimal number into fractions. The quotient is used in the multiplication of two whole numbers: for example, 4×5=20, which was simplified from $4 \times 5=20\Rightarrow \dfrac{(4 \times 10)}{2}$.
Solved Examples
Q 1 Divide 217 by 4.
Ans: $\dfrac{217}{4}$
Here, Dividend = 217
Divisor = 4
Quotient = 54
Remainder = 1
Q 2 Find the remainder when the dividend is 75, the divisor is 5 and the quotient is 15.
Ans: Given, dividend = 75, divisor = 5, quotient = 15 and let the remainder be x
75 = 5 × 15 + x
75 = 75 + x
x = 75 - 75
x = 0
Therefore, by using the formula we obtained the remainder which is 0. Remainder = 0
Q 3 Find the remainder when the dividend is 63, the divisor is 2 and the quotient is 31.
Ans: Given, dividend = 63, divisor = 2, quotient = 31 and let the remainder be x
63 = 2 × 31 + x
63 = 62 + x
x = 63 - 62
x = 1
Q 4 Divide 5679 by 7.
Ans: $\dfrac{5679}{7}$
Here, Dividend = 5679
Divisor = 7
Quotient = 811
Remainder = 2
Q 5 Find the remainder when the dividend is 57, the divisor is 8 and the quotient is 7.
Ans: Given, dividend = 75, divisor = 5, quotient = 15 and let the remainder be x
57 = 8 × 7 + x
57 = 56 + x
x = 57 -56
x = 1
Therefore, by using the formula we obtained the remainder which is 1. Remainder =1
Practice Questions
Q 1 Divide 120 by 5 and find the quotient and the remainder.
Ans: Quotient = 24
Remainder = 0
Q 2 Find the dividend when the remainder is 1, the divisor is 3, and the quotient is 31.
Ans: Dividend = 94
Q 3 Find the remainder when the dividend is 55, the divisor is 3 and the quotient is 18.
Ans: Remainder = 1
Summary
In conclusion, the number which is getting divided here is called the dividend. The number which divides a given number is the divisor. Also, the number which we get as a result is known as the quotient. The divisor which does not divide a number completely produces a number, which is referred to as remainder. We now hope you have a clear understanding of divisor, dividend, quotient and remainder.
FAQs on Divisor, Dividend, Quotient, and Remainder Made Easy
1. What are the four main components of a division problem?
In any division problem, there are four main components that describe the numbers involved:
- Dividend: The number that is being divided.
- Divisor: The number by which the dividend is being divided.
- Quotient: The result or the answer obtained after the division.
- Remainder: The value left over after the division is complete. It is always less than the divisor.
2. What is the fundamental formula that connects the dividend, divisor, quotient, and remainder?
The relationship between these four components is defined by the Division Algorithm formula. This formula is used to verify the result of a division. The formula is: Dividend = (Divisor × Quotient) + Remainder. This equation must hold true for any division operation.
3. Can you explain dividend, divisor, quotient, and remainder with a simple, real-life example?
Certainly. Imagine you have 25 sweets (the Dividend) and you want to share them equally among 4 friends (the Divisor). Each friend would get 6 sweets (the Quotient). After sharing, you would have 1 sweet left over (the Remainder) because 4 goes into 25 six times (4 × 6 = 24), with 1 remaining.
4. How can you find the dividend if the divisor, quotient, and remainder are known?
You can find the original number (the dividend) by using the division formula: Dividend = (Divisor × Quotient) + Remainder. For example, if the divisor is 7, the quotient is 5, and the remainder is 3, you can calculate the dividend as follows: Dividend = (7 × 5) + 3 = 35 + 3 = 38.
5. What are the special rules for division when the dividend or divisor is zero?
Using zero in division has specific rules that are very important to remember:
- When the dividend is 0: If you divide zero by any non-zero number, the quotient is always 0 (e.g., 0 ÷ 5 = 0).
- When the divisor is 0: Division by zero is undefined in mathematics. You cannot divide any number by 0, as it doesn't yield a meaningful result.
6. Is the remainder always smaller than the divisor? What happens if it's not?
Yes, it is a fundamental rule of division that the remainder must always be smaller than the divisor. If your calculated remainder is equal to or larger than the divisor, it means the division is incomplete. You need to increase the quotient, as the divisor can fit into the dividend at least one more time.
7. How is the concept of a remainder useful in real-life situations?
The remainder is extremely useful in many practical scenarios beyond the classroom. For example, it helps in:
- Grouping items: Figuring out how many items are left over after creating equal groups, like seating students in rows or packing items in boxes.
- Scheduling: Calculating remaining days or hours after dividing a total period into weeks or days.
- Resource allocation: Determining leftover resources after distributing them equally among a number of people or projects.
8. How can you express the result of a division that has a remainder as a mixed number?
When a division results in a non-zero remainder, you can write the exact answer as a mixed number. The quotient becomes the whole number part, the remainder becomes the numerator, and the original divisor becomes the denominator. For example, 25 ÷ 4 gives a quotient of 6 and a remainder of 1. As a mixed number, this is written as 6 1/4.
