




Overview of the Comparison of Unlike Fractions
There are several ways we use fractions unknowingly while performing our day to day activities. It is fair to say that the world would not be without fractions as we see it today. One can compare fractions with unlike denominators by finding the least common denominator, or the smallest multiple the denominators share. Then we tend to make equivalent fractions, or fractions that represent the constant part of the total. As an example $\dfrac{1}{2}, \dfrac{1}{3}, \dfrac{1}{4}, \dfrac{1}{5}$ these are unlike fractions.
What is Fraction?
The terms used to determine the parts of a whole object are called fractions. For example, a pizza is divided into 4 pieces, so each piece of it is represented as $\dfrac{1}{4}$th of the pizza. Here 1 will be the numerator and 4 will be the denominator.
Types of Fraction
On the basis of numerator and denominator, apart from these three main types of fractions, there are three more types of fractions namely like & unlike fractions and equivalent fractions. Hence, there are total 6 types of fractions such as:
Proper Fraction
Mixed Fraction
Like Fractions
Unlike Fractions
Equivalent Fractions
Note: The primary three fractions are defined for a single fraction however the other three fractions determine the comparison between two or more fractions.
Unlike Fractions
Unlike fractions, fractions which have unequal denominators or different denominators. As an example $\dfrac{1}{2}, \dfrac{1}{3}, \dfrac{1}{4}, \dfrac{1}{5}$, were unlike fractions.
Simplification for such fractions is a little lengthy method since we need to factorize the denominator first and then simplify them (in case of addition and subtraction).
Suppose, we have to add $\dfrac{1}{2}$ and $\dfrac{1}{3}$. First of all we will find the LCM of 2 and 3 which is equal to 6.
Then we will multiply $\dfrac{1}{2}$ by 3 and $\dfrac{1}{3}$ by 2, in both the numerator and denominator.
The fractions will become $\dfrac{3}{6}$ and $\dfrac{2}{6}$.
Then, if $\dfrac{3}{6}$ and $\dfrac{2}{6}$ are added , we get;
$\dfrac{3}{6}+\dfrac{2}{6}=\dfrac{5}{6}$
Comparing Fractions
To compare unlike fractions, we change the unlike fractions to like fractions and then compare.
On comparison of two fractions with equal numerator,
$\dfrac{4}{7} \text { and } \dfrac{4}{9}$ whose numerator is the same.
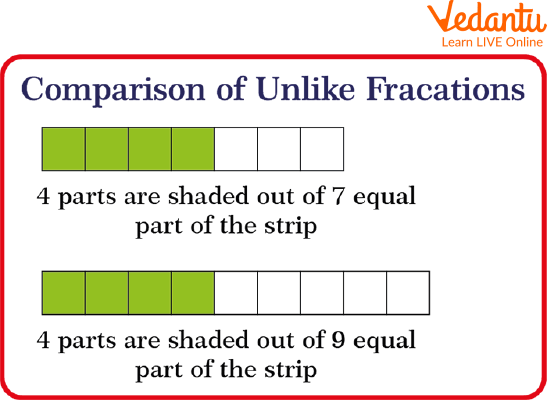
Comparison of unlike fractions
Since 4 shaded elements of 7 is larger than the 4 shaded elements of 9 thus, $\dfrac{4}{7}>\dfrac{4}{9}$
To compare two fractions with totally different numerators and denominators, we multiply by a number to convert them into like fractions.
Solved Examples
Q 1. Which one is greater, $\dfrac{4}{7}$ Or $\dfrac{3}{5}$
Ans: First we convert these fractions into like fractions. To convert unlike fractions into like fractions first of all find the L.C.M. of their denominators.
L.C.M. of 7 and 5 will be $=35$
Now, On dividing the L.C.M. by the denominator of both fractions.
$35 \div 7=5$
$35 \div 5=7$
On Multiplying both the numerator and denominator with the number we get after dividing.
i.e.,
$\dfrac{4 \times 5}{7 \times 5}=\dfrac{20}{35}$
$\dfrac{3 \times 7}{5 \times 7}=\dfrac{21}{35}$
because, $\dfrac{21}{35}>\dfrac{20}{35}$ (because the denominator is the same and hence by checking the numerator, $21>20)$
So,
$\dfrac{3}{5}>\dfrac{4}{7}$
One can compare the two fractions by cross multiplication method also.
On solving the above example by cross multiplication. We will cross-multiply as follows.
$4 \times 5=20$
$3 \times 7=21$
Since, $21>20$
Therefore, $\dfrac{3}{5}>\dfrac{4}{7}$
Practice Questions
Write the correct comparison symbol.
Q 1. $\dfrac{2}{10} \square \dfrac{2}{5}$
Ans: $\dfrac{2}{10} < \dfrac{2}{5}$
Q 2. $\dfrac{1}{10} \square \dfrac{1}{5}$
Ans: $\dfrac{1}{10} < \dfrac{1}{5}$
Q 3. $\dfrac{3}{4} \square \dfrac{4}{7}$
Ans: $\dfrac{3}{4} > \dfrac{4}{7}$
Summary
In this Article about unlike fractions we have learnt that one can compare fractions with unlike denominators by finding the least common denominator, or the smallest multiple the denominators share. Then we tend to make equivalent fractions, or fractions that represent the constant part of the total And practice questions which will help to grasp the topic more easily. This blog shed light on fractions and how they are applied in different mathematics branches and how they impact our everyday life.
FAQs on Comparison of Unlike Fractions
1. What does it mean to compare unlike fractions in Maths?
Comparing unlike fractions means determining which fraction represents a greater or smaller part of a whole when their denominators are different. This is done by converting the fractions to have a common denominator, making comparison straightforward as both fractions then refer to equal-sized parts.
2. How do you convert unlike fractions to like fractions for comparison?
To convert unlike fractions to like fractions, first find the least common multiple (LCM) of their denominators. Rewrite each fraction with the LCM as the new denominator by multiplying both numerator and denominator accordingly. This ensures both fractions are expressed with the same-sized parts, making them easier to compare.
3. Can you explain the cross-multiplication method for comparing two unlike fractions?
With cross-multiplication, multiply the numerator of the first fraction by the denominator of the second, and the numerator of the second by the denominator of the first.
- If the result of the first multiplication is greater, the first fraction is larger.
- If the second is greater, the second fraction is larger.
4. Why is finding a common denominator necessary for comparing unlike fractions?
Finding a common denominator makes the fractions refer to equal parts of the whole. This eliminates confusion from having differently sized divisions, allowing you to compare the numerators directly and determine which fraction is greater or smaller.
5. What types of errors do students commonly make when comparing unlike fractions?
Common errors include comparing only numerators or denominators without adjusting for a common denominator, or neglecting to properly multiply both numerator and denominator. It's important to always ensure both fractions are written using the same denominator before comparing numerators, or to use the cross-multiplication rule correctly.
6. How can comparison of unlike fractions help in solving real-life problems?
Many real-life scenarios, such as dividing resources, cooking, or measuring, require comparing unequal parts. Understanding how to compare unlike fractions helps in making logical decisions about proportions, quantities, and fair division in everyday activities.
7. What are the steps to add or subtract unlike fractions?
To add or subtract unlike fractions:
- Find the LCM of the denominators.
- Convert each fraction to an equivalent fraction with the LCM as the denominator.
- Add or subtract the numerators, keeping the denominator the same.
- Simplify the result if possible.
8. How do you know if two fractions are like or unlike?
Two fractions are like if they have the same denominator, and unlike if their denominators are different. For example, 1/3 and 2/3 are like; 1/3 and 1/4 are unlike.
9. What are equivalent fractions, and how are they related to comparison of unlike fractions?
Equivalent fractions are different fractions that represent the same value or portion of a whole. When comparing unlike fractions, we often convert them to equivalent forms with common denominators to make comparison possible.
10. If two fractions have the same numerator, how do you decide which is greater?
For fractions with the same numerator, the one with the smaller denominator is always greater, since each part is larger. For example, 4/7 > 4/9 because sevenths are larger than ninths when you have the same number of parts.
11. Why might the comparison of unlike fractions appear in CBSE board exams?
Understanding comparison of unlike fractions is a foundational concept in Maths and often appears in CBSE board exams because it tests comprehension of rational numbers, number operations, and logical reasoning, which are key areas of the official 2025–26 syllabus.
12. Can you give an example where cross-multiplication and common denominator methods both work for comparing two fractions?
Yes, for 3/5 and 4/7:
- Common denominator: convert both to denominator 35: 3/5 = 21/35, 4/7 = 20/35, so 3/5 > 4/7.
- Cross-multiplication: 3 × 7 = 21, 4 × 5 = 20; since 21 > 20, 3/5 is greater.











