




How to Apply the Addition Theorem of Probability in Problems
Probability defines the likelihood of an event occurring. There are many situations in real life where we may need to predict the outcome of an event. We may or may not be certain of the outcome of the event. In such cases, we say that there is a probability that the event will or will not occur. Probability in general has great applications in games, and in business for making predictions based on probability, and also probability has extensive applications in this new field of artificial intelligence.
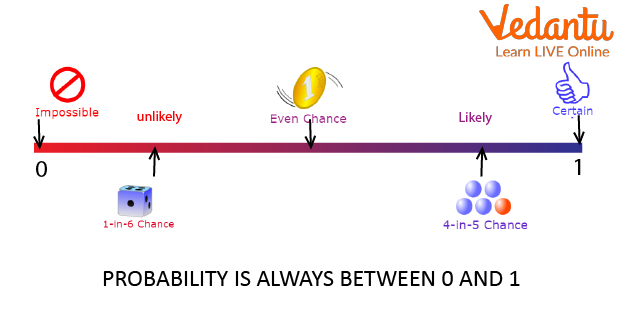
The probability of an event can be calculated using the probability formula simply by dividing the number of favorable outcomes by the total number of possible outcomes. The probability value of an event occurring can lie between 0 and 1, since the number of favourable outcomes can never exceed the total number of outcomes. Also, a favorable number of results cannot be negative. Let's discuss the basics of probability in detail in the following sections.
Theory of Probability
Probability can be defined as the ratio of the number of favorable outcomes to the total number of outcomes of an event. For an experiment that has "n" number of outcomes, the number of favorable outcomes can be denoted by x. The formula for calculating the probability of an event is as follows.
Probability(Event) = Favorable Outcomes/Total Outcomes = x/n
Probability
Additional Theorem With Example
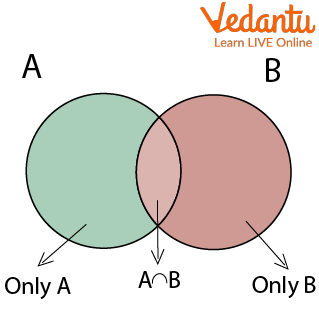
If $A$ and $B$ are any two events of a random experiment and $P$ is a probability function then the probability of happening of at least one of the events is defined as $P(A \cup B)=P(A)+P(B)-P(A \cap B)$.
Now, we have to prove the Addition theorem of probability.
Given: A and B are any two events of a random experiment.
To prove: $P(A \cup B)=P(A)+P(B)-P(A \cap B)$.
Proof:
From the set theory we know that
$n(A \cup B)=n(A)+n(B)-n(A \cap B)$
Suppose $n(S)$ denote the total number of the possible events of random experiment and then dividing both left hand side and right hand side of the of the above equation we get,
$\frac{P(A \cup B)}{n(S)}=\frac{P(A)}{n(S)}+\frac{P(B)}{n(S)}-\frac{P(A \cap B)}{n(S)}$
Now, we know that a formula for probability $P(x)=\frac{n(x)}{n(S)}$. By applying this we can write
$P(A \cup B)=P(A)+P(B)-P(A \cap B)$
Hence, the above given additional theorem of probability is proved.
Additional Theorem Of Probability
Examples:
As per the expansion hypothesis, if two occasions A and B are fundamentally unrelated, the probability of one or the other A or B happening is all out of the singular probabilities of A and B.
For two fundamentally unrelated occasions A, B
P(A or B)=P(A)+P(B)
Example for addition theorem of probability for 3 events: If $A, B$ and $C$ are three events in the sample space $S$. Then,
$P(A \cup B \cup C)=P(A)+P(B)+P(C)-P(A \cap B)-P(B \cap C)-P(C \cap A)+P(A \cap B \cap C)$
If $\mathrm{A}, \mathrm{B}$ and $\mathrm{C}$ are three mutually exclusive events, then
$P(A \cup B \cup C)=P(A)+P(B)+P(C)$
Summary
Probability is a branch of mathematics concerned with numerical descriptions of how likely an event is to occur or how likely a statement is to be true. The probability of an event is a number between 0 and 1, where, roughly speaking, 0 indicates the impossibility of the event and 1 indicates certainty.
FAQs on Addition Theorem of Probability Explained
1. What is the Addition Theorem of Probability and how is it expressed for two events?
The Addition Theorem of Probability states that for any two events A and B, the probability of at least one occurring is P(A ∪ B) = P(A) + P(B) – P(A ∩ B). This formula is used to find the probability that either event A or event B or both occur in a random experiment.
2. How does the Addition Theorem of Probability change for mutually exclusive events?
When two events are mutually exclusive (cannot happen together), the probability of both occurring is zero, so the formula simplifies to P(A ∪ B) = P(A) + P(B). This is because P(A ∩ B) = 0 for mutually exclusive events.
3. Why is the subtraction term – P(A ∩ B) necessary in the Addition Theorem?
The term –P(A ∩ B) prevents double counting the outcomes that are common to both A and B. Without it, the overlap would be included twice, giving an incorrect total probability.
4. Can the Addition Theorem be extended to three events? If yes, what does the formula look like?
Yes, for three events A, B, and C, the addition theorem is:
- P(A ∪ B ∪ C) = P(A) + P(B) + P(C) – P(A ∩ B) – P(B ∩ C) – P(C ∩ A) + P(A ∩ B ∩ C)
5. What types of errors do students commonly make when applying the Addition Theorem of Probability?
Common errors include:
- Forgetting to subtract P(A ∩ B) when events are not mutually exclusive
- Assuming events are always mutually exclusive without checking conditions
- Incorrectly identifying the intersection set
- Miscalculating probability values for events with overlap
6. How is the Addition Theorem of Probability applied to solve real-life problems?
The theorem is used in situations where two or more events can overlap, such as finding the probability that a card drawn from a deck is either red or a king, or that a person selected speaks English or French. It helps in correctly adding probabilities without overcounting shared outcomes.
7. What is a typical difference between mutually exclusive and independent events in the context of the addition theorem?
Mutually exclusive events cannot happen together (P(A ∩ B) = 0), so the addition theorem omits the intersection term. Independent events can occur simultaneously with P(A ∩ B) = P(A) × P(B), which is considered in the addition theorem unless events are mutually exclusive.
8. How does the addition theorem help in answering HOTS (Higher Order Thinking Skills) questions in board exams?
It requires students to identify overlapping probabilities and calculate the correct union value, which tests conceptual clarity. HOTS questions may combine the addition theorem with Venn diagrams or word problems, challenging students to apply the concept beyond rote use.
9. What should be checked before applying the Addition Theorem to a particular problem?
Before application, check if the events are mutually exclusive or not, understand the sample space fully, and confirm if the overlap P(A ∩ B) can be directly calculated or needs additional analysis based on the problem statement.
10. If P(A) = 0.4, P(B) = 0.3, and P(A ∩ B) = 0.1, what is the probability that either event A or B occurs?
Using the addition theorem:
- P(A ∪ B) = P(A) + P(B) – P(A ∩ B) = 0.4 + 0.3 – 0.1 = 0.6















