




What Is the Formula for the Time Period of a Simple Pendulum?
The time period of a simple pendulum is a fundamental concept in oscillatory motion. It describes how long a pendulum takes to complete one full swing, and understanding this helps students master the basics of periodic motion in physics. In this article, we’ll explore the definition, formula, important dependencies, and practical aspects you need for the JEE syllabus or board exams.
What is the Time Period of a Simple Pendulum?
The time period is the time the pendulum bob takes to return to its starting position after finishing one complete oscillation. For any simple pendulum, this value remains the same for each cycle under ideal conditions. This concept closely relates to simple harmonic motion, which is key to understanding oscillations and waves in physics.
Time Period of Simple Pendulum: Definition and Formula
The standard formula for the time period of a simple pendulum shows how it depends on length and gravity, not on mass or material of the bob. If you are asked to write the time period of simple pendulum formula for class 7 or JEE, use:
| Quantity | Symbol (SI Unit) |
|---|---|
| Time Period | T (s) |
| Length of String | l (m) |
| Accel. due to Gravity | g (m/s²) |
The formula for the time period of a simple pendulum is:
T = 2π√(l/g), where l is the length of the string and g is the local acceleration due to gravity. This equation is essential in both the time period of simple pendulum formula for class 7 and class 11 levels.
Stepwise Derivation: Time Period of Simple Pendulum
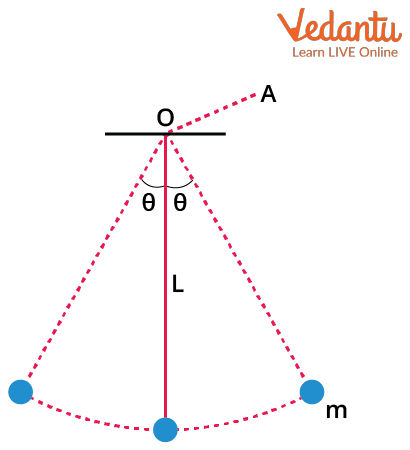
Let’s derive the time period of a simple pendulum, as commonly required for class 11 and entrance exams. The derivation uses Newton’s laws and small angle approximation, where sin θ ≈ θ (in radians).
Consider a simple pendulum of mass m and length l swung at a small angle θ. The restoring torque (τ) about the suspension point is:
τ = –mglθ
From rotational dynamics: Iα = τ
The moment of inertia (I) for a point mass about its suspension is ml².
Angular acceleration (α) is d²θ/dt².
So, ml²(d²θ/dt²) = –mglθ
After rearrangement: d²θ/dt² + (g/l)θ = 0
This is the form of a simple harmonic oscillator, where angular frequency (ω) = √(g/l).
The time period of oscillation is thus: T = 2π/ω = 2π√(l/g).
This stepwise time period of simple pendulum derivation for class 11 and competitive exams shows the formula is valid for small angular displacements.
Factors Affecting the Time Period of a Simple Pendulum
Students often ask which variables influence the time period and which do not. Here’s a concise effect table:
| Factor | Effect on T |
|---|---|
| Length of string (l) | Direct (T ∝ √l) |
| Acceleration due to gravity (g) | Inverse (T ∝ 1/√g) |
| Mass of bob | No effect |
| Amplitude (small angles) | No effect if θ ≤ 5° |
| Material/Shape (ideal case) | No effect |
The time period of simple pendulum is independent of the bob’s mass and (for small displacements) amplitude. Larger amplitudes (over 15°) can make the period increase slightly due to non-linear motion.
Time Period of Simple Pendulum: Graphical Insight and Infinite Length
If you graph T² against l, you get a straight line, confirming that T² ∝ l. This linear relationship is frequently used in lab experiments. An interesting theoretical concept is the time period of a simple pendulum of infinite length—if l → ∞, then T → ∞, meaning the pendulum would never complete an oscillation. This scenario is a mathematical abstraction but helps visualize the direct dependence on length.
Key Characteristics and Properties
The simple pendulum exhibits these classic characteristics in oscillatory systems:
- The motion is periodic and regular
- For small angles, it behaves as a simple harmonic oscillator
- Time period does not depend on mass or amplitude (if amplitude small)
- Restoring force proportional to displacement
- The concept is crucial for topics like simple harmonic motion
- Dimensionally, T has the dimension [T]
These features are also explained in greater detail in topics like Simple Harmonic Motion, helping you connect pendulum concepts to other oscillatory phenomena.
Experimental Setup and Typical Procedure
To determine the time period experimentally, set up a clamp stand, attach a light string and bob, and measure the string from the point of suspension to the bob’s center. Displace the bob through a small angle and release it to swing freely.
Use a stop-watch to time n complete oscillations (commonly 20 or 50), then calculate the time period as T = total time / n. Repeat by adjusting string length for accuracy and to validate relationship with length. This method directly demonstrates the time period of simple pendulum for class 7 and 11 curricula.
A simple pendulum diagram showing bob, string, and oscillating motion can clarify the physical setup for students new to the concept.
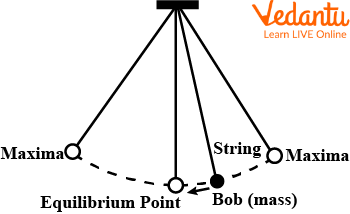
Common errors in this experiment stem from large amplitude swings, parallax, inaccurately counting oscillations, and not measuring string length from the exact suspension point. Reducing air resistance and ensuring minimal friction help increase the precision of your observations.
Summary Table: Essential Points for the Time Period Concept
A concise summary makes for easy revision before any exam. Find the main points related to the time period of simple pendulum formula and dependencies below:
| Point | Quick Recap |
|---|---|
| Formula | T = 2π√(l/g) |
| Dimension | [T] |
| Depends on | Length, gravity |
| Independent of | Mass, (small) amplitude |
| Major source of error | Parallax, counting, amplitude |
| Typical clock pendulum | Seconds pendulum (T = 2 s) |
Uses and Relevance in Everyday Physics
The time period of simple pendulum is not just an academic concept—it supports the design of pendulum clocks, experimental determination of gravitational acceleration, and basic demonstrations of periodic motion in the classroom. The seconds pendulum (T = 2s) even helped define the modern second, showing the lasting impact of this simple result.
You can further connect this knowledge with related topics like Oscillations And Waves when preparing for advanced study. Vedantu often revisits foundational pendulum material because it links so many major physics themes.
A simple pendulum and axis of rotation for time period can also improve your grasp of experimental setup and practical calculation.
Conclusion: Mastering the Time Period Formula
Knowing and understanding the time period of simple pendulum formula, as well as its derivation and dependencies, is essential for board exams and competitive tests alike. Remember that the time period increases with string length, decreases with stronger gravity, and remains unchanged by mass or small amplitude. Practicing these fundamentals is the best way to ensure confidence in exam questions related to this core topic.
For deeper insight, explore the Time Period Of Simple Pendulum topic page and related resources on Vedantu. Understanding these relationships will build a strong physics foundation for future studies and practical applications.
FAQs on Understanding the Time Period of a Simple Pendulum
1. What is the time period of a simple pendulum?
The time period of a simple pendulum is the time taken to complete one full oscillation or swing.
Key points include:
- The formula is T = 2π√(l/g), where l is the length of the pendulum and g is acceleration due to gravity.
- The time period depends on the length of the string and value of gravity, not on mass or amplitude (for small angles).
2. What is the formula for the time period of a simple pendulum?
The formula for the time period (T) of a simple pendulum is T = 2π√(l/g).
Where:
- T = Time period (seconds)
- l = Length of the pendulum (metres)
- g = Acceleration due to gravity (9.8 m/s2 on Earth)
3. Which factors affect the time period of a simple pendulum?
The time period of a simple pendulum mainly depends on the length of the string and acceleration due to gravity.
The main factors are:
- Length (l): The time period increases as the length increases.
- Acceleration due to gravity (g): The time period decreases with an increase in gravity.
4. Does the mass of the bob affect the time period of a simple pendulum?
No, the mass of the pendulum bob does not affect its time period.
Key reasons:
- The formula T = 2π√(l/g) does not include mass.
- The time period depends only on the length of string (l) and gravity (g).
5. How does the length of a simple pendulum affect its time period?
The time period increases as the length of the simple pendulum increases.
According to the formula T = 2π√(l/g):
- If the length (l) increases, T increases.
- If the length is doubled, time period increases by √2 times.
6. Why does a pendulum stop swinging after some time?
A pendulum stops swinging due to the loss of energy from air resistance and friction.
The main reasons include:
- Air resistance slows down the motion and reduces amplitude.
- Friction at the pivot absorbs kinetic energy.
7. What is the effect of gravity on the time period of a simple pendulum?
An increase in gravity (g) decreases the time period (T) of a simple pendulum.
Considerations:
- The time period is inversely proportional to the square root of g (T ∝ 1/√g).
- On the Moon (lower gravity), pendulums swing slower (longer T) than on Earth.
8. What are the applications of simple pendulum in daily life?
Simple pendulums are used to measure time and study motion in real life.
Applications include:
- Pendulum clocks
- Seismometers
- Calibrating time-keeping devices
- Demonstrating concepts of periodic and simple harmonic motion in laboratories
9. Explain why the time period of a simple pendulum is independent of amplitude for small angles.
For small angles (less than 15°), the time period (T) of a simple pendulum is independent of amplitude.
Main reasons:
- The formula T = 2π√(l/g) is derived using the small angle approximation, where amplitude does not appear.
- At small angles, the restoring force is directly proportional to displacement, resulting in simple harmonic motion.
10. What is meant by oscillation in the context of a simple pendulum?
Oscillation in a simple pendulum refers to one complete back and forth motion from one extreme to the other and back again.
Key features:
- One oscillation is one full swing (A → B → A).
- Time period is the duration of one oscillation.
- This movement is an example of periodic motion.


































